This post shows how the core trigonometric definitions, relations and addition theorems can be simply and intuitively visualized.
First published: 8th Feb, 2019
Last modified: 9th May, 2020
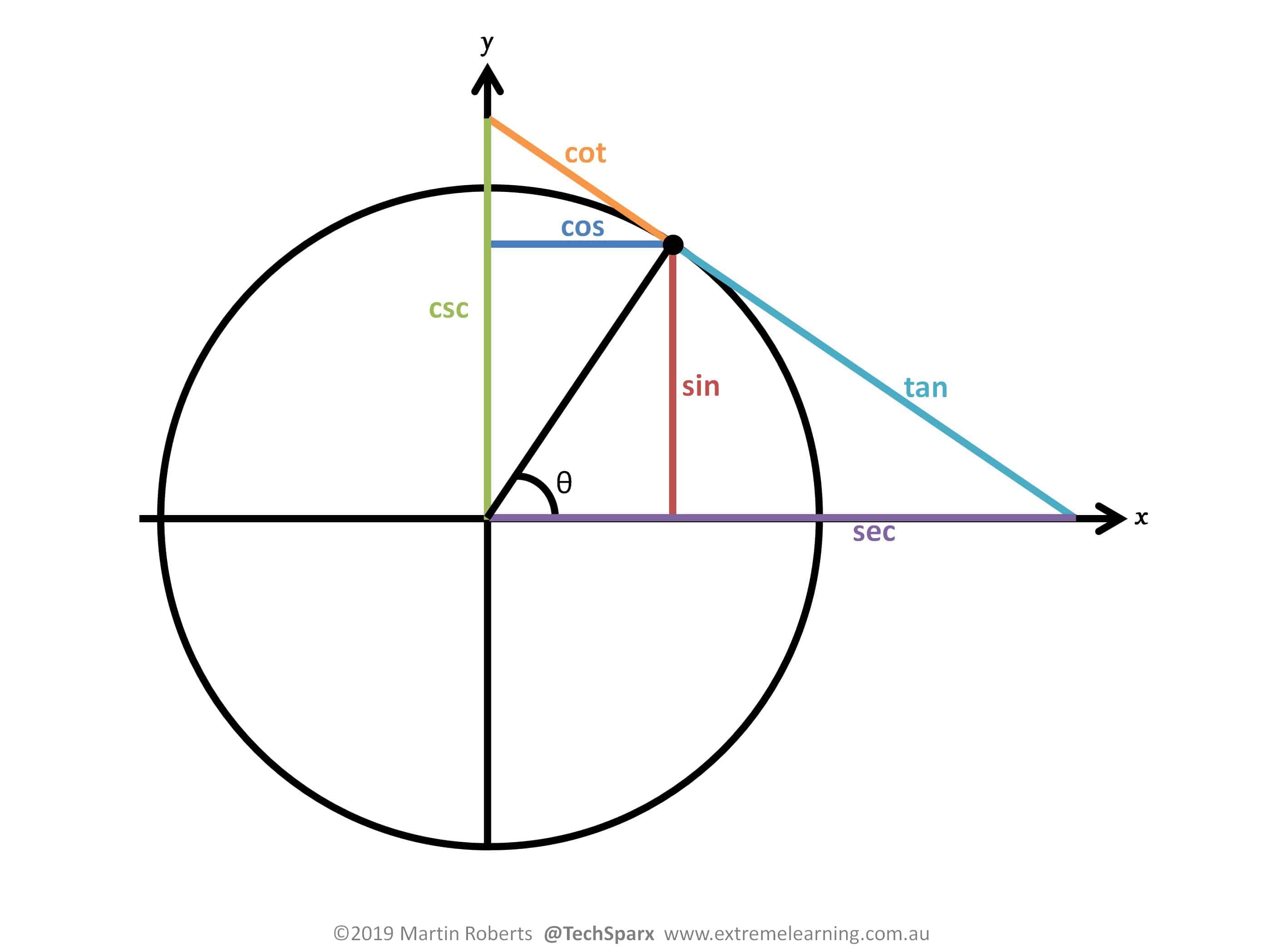
Note that most of us learnt that the definitions of $\sec, \csc, \cot$ were $1/\cos, 1/\sin, 1/\tan$, respectively.
However, from a historical and geometrical point of view, this is not quite true.
Etymologically, the word sine derives from the Sanskrit for ‘chord’, and so the sin(.) function is defined as the length of the chord subtended by the angle theta within a unit circle.
Now also historically, if theta is the angle the radial line makes with the x-axis, then the angle it makes with the y-axis is called the complementary angle (and is thus equal to 90-theta).
Thus, in figure 1, we see that more clearly the origin of the term cos, which is short for cosine which in turn is short for the sine of the complementary angle (90-theta). That is, the length of the chord in a unit circle subtended by the complementary angle.
And finally tan is short for ‘tangent‘, and thus the tan(.) function is defined in terms of the length of the tangent at angle to the unit circle.
And for completeness,
- sec is short for secant is derived from the word ‘cut’ and represents the segment that cuts the x-axis from the tangent.
- csc(.) which is short for cosec(.) which in turn is short for cosecant, which in turn is short for secant of the complementary angle.
- cot(.) is short for cotangent, which is turn short for tangent of the complementary angle.
In the above diagram, the 3 classic trigonometric identities are now obvious:
$$ \sin^2 \theta + \cos^2 \theta = 1; \quad \quad 1+\tan^2 \theta = \sec^2 \theta; \quad \quad 1+\cot^2 \theta = \csc^2 \theta $$
And now here is the connection from the historical definitions based on lengths, to the modern defintions based on ratios….
Suppose the circle was not a unit circle but a circle with a radius h.
Then you should be able to see that all the lengths of all the triangles in the diagram are increased by a factor of h.
Thus, the length of the chord would not be sin(.) anymore, but h*sin(.)
However, what is beautiful is that the ratio of the length of this chord to the radius h, remains a constant value of h*sin(theta)/h = sin(theta).
And in this form, you will hopefully recognize the connection with the more familiar ratio of opp/hyp = sin(theta).
Thus, the trigonometric ratios as you have memorised are a statement that if the circle is enlarged to arbitray size, then the ratio of the side lengths of key right-angled triangles remains constant.
For the example given above, the constant of proportionality is given by sin(.)
Similar argument for cos(.) and almost similar argument for tan(.)
An alternative to the above version.
In this version all those on the lower-right hand side of the radial line (sin, tan, sec) are associated with the angle $\theta$.
And all those on the upper-left hand side of the radial line (cosine, cotan, cosec) are associated with the complementary angle $90-\theta$.
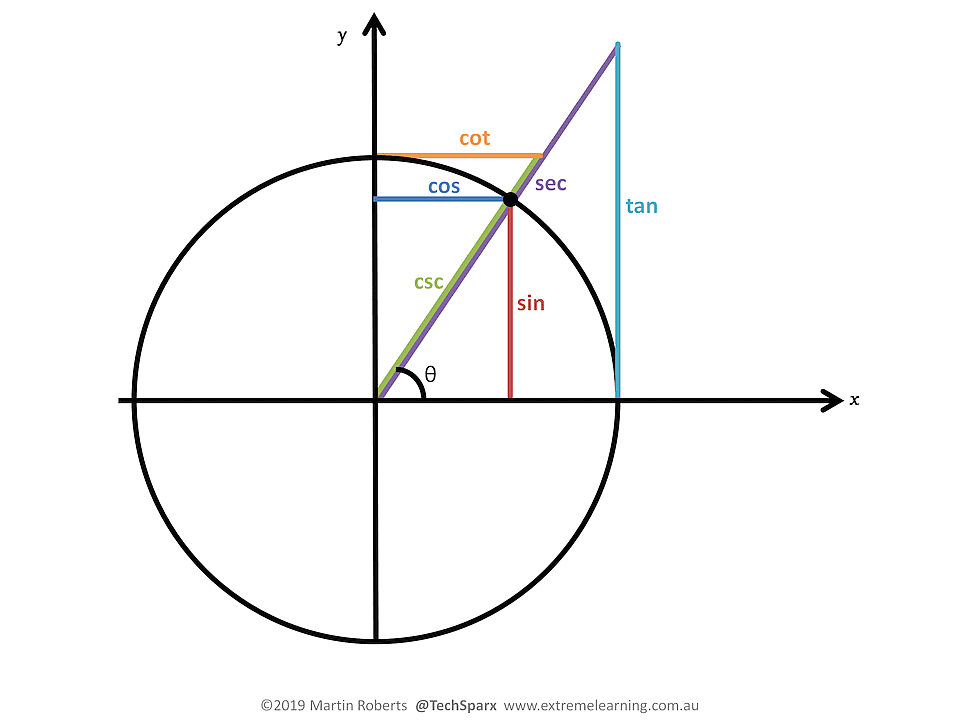
Note that in both of them you learn that the tan function is intimately related to the tangent of a circle, and not just the ratio “opposite over hypotenuse’.
Hyperbolic Trig Functions
Unfortunately there is not a single diagram that as succinctly shows the analogous hyperbolic relationships and identities
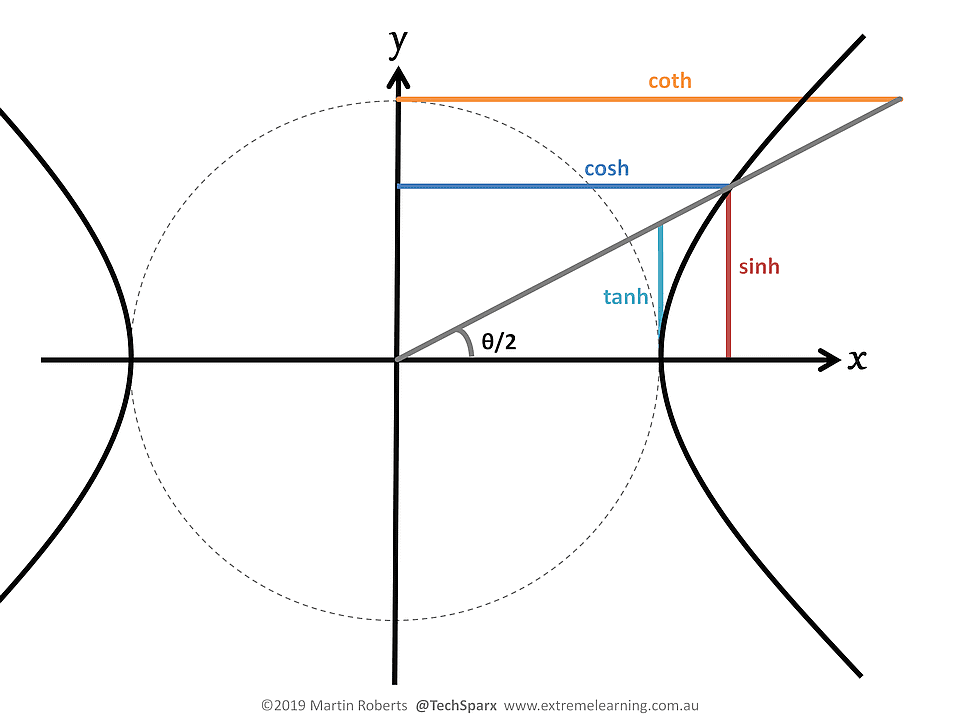
From this diagram, we can clearly see $ \cosh^2 \theta – \sinh^2 \theta = 1 $, but the other two hyperbolic trig identities are not so obvious.
![]()
Figure 3. Hyperbolic Functions. This presents a direct analogy of figure 2.
See here for some other good versions.
Addition Theorems
Looking at the vertical sides, we have: $\sin(\alpha+\beta) = \sin \alpha \; \cos \beta + \cos \alpha \; \sin \beta$.
And comparing the horizontal sides, we have: $\cos(\alpha+\beta) = \cos \alpha \; \cos \beta – \sin \alpha \; \sin \beta$.
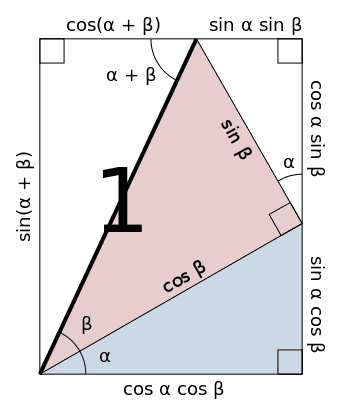
The white triangle on the left-hand side shows: $$\tan (\alpha + \beta) = \frac{\tan \alpha +\tan \beta}{1-\tan \alpha \tan \beta} $$.
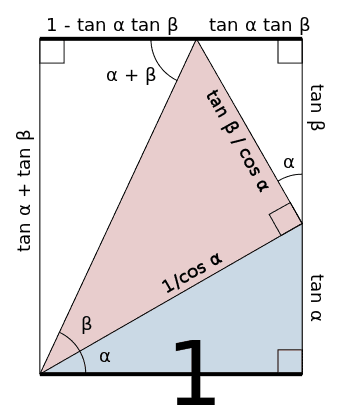
The following diagram assists in understanding why
$\cos 2 \alpha = \cos^2 \alpha – \sin^2 \alpha $$
and
$\sin^2 \alpha = 2 \sin \alpha \; \cos \alpha.$
![]()
My name is Martin Roberts. I have a PhD in theoretical physics. I love maths and computing. I’m open to new opportunities – consulting, contract or full-time – so let’s have a chat on how we can work together!
Come follow me on Twitter: @Techsparx!
My other contact details can be found here.
[mc4wp_form id=”1021″]
A very nice collection of mathematical gems that are hard to find when you need them. I really enjoyed every single page; hope you keep the spirit up.
Thank you so much for these encouraging words. Sometimes I find it hard to keep writing as I don’t feel it comes naturally to me, so your kind words are very much appreciated. 🙂
Thank you Martin for this post, I very much appreciate it. As someone who struggles with Trigonometry due to shaky foundations this exactly what I needed. Cheers.
The label in the hyperbolic function diagrams for the hyperbolic angle is rather misleading, as it seems to imply that theta/2 is an ordinary angle, rather than the area bounded by the hyperbolic sector.