Category: multi-armed bandits

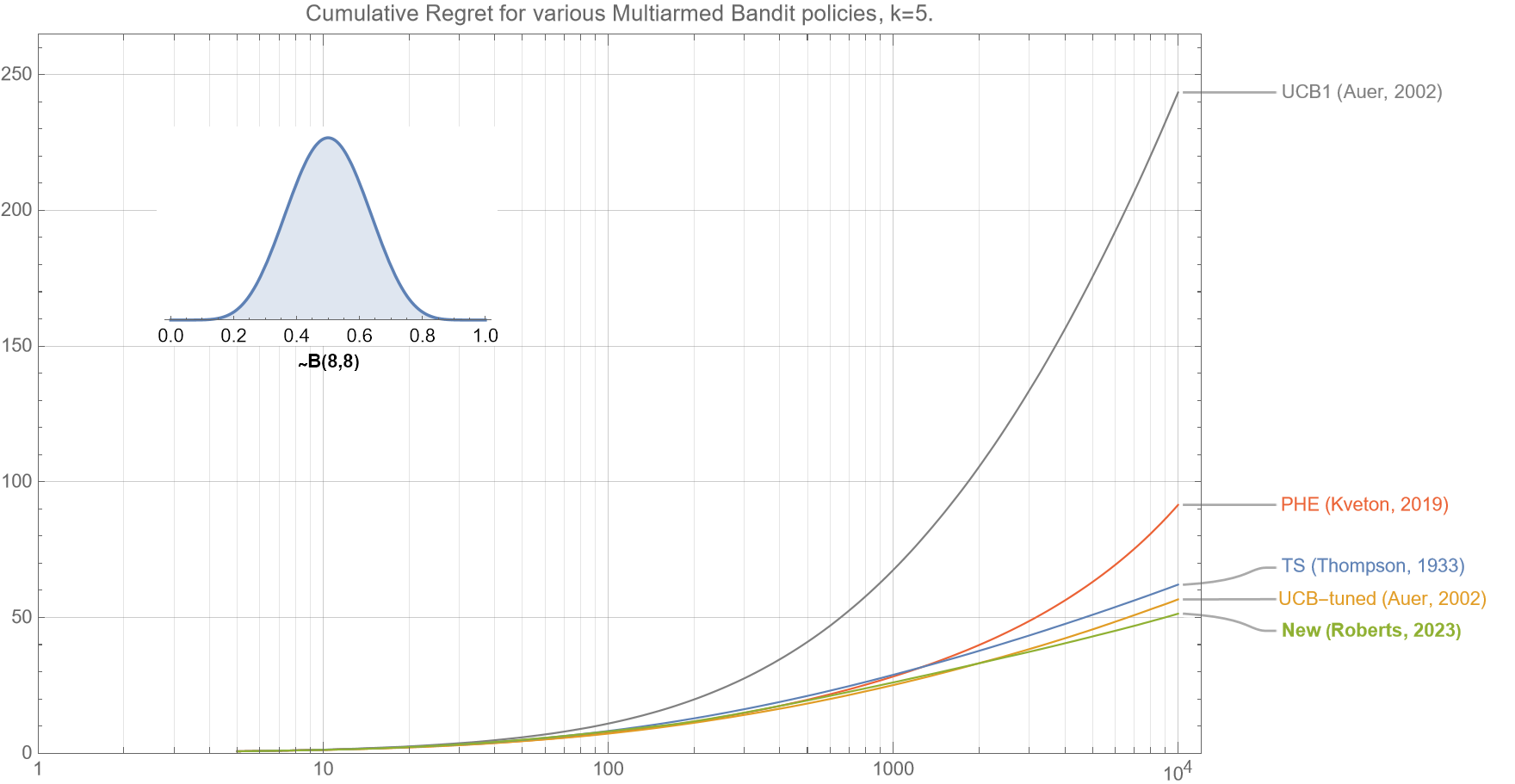
I propose a new algorithm for multi-armed bandits that is fully deterministic, as fast and simple to implement as UCB1, and yet, for a very broad range of practical circumstances empirically outperforms many of the existing industry standard Bernoulli multi-armed bandit policies, including Thompson Sampling and UCB1 and UCB-tuned.

Cumulative Regret for various multi-armed bandit policies. — **Figure 1.** This comparison of various bandit policies shows that if the underlying probabilities for the $k=5$ arms are drawn from a beta distribution $B(8,8)$, then the cumulative regret curve (smaller is better) for our new algorithm (as described in section 2.5) outperforms *UCB1*, *UCB-tuned*, *Perturbed History Exploration (PHE*), and *Thompson Sampling* for almost all $t<10^4$.

Continue reading “Improving on the UCB1 multi-armed bandit algorithm”