Always curious. Always learning.
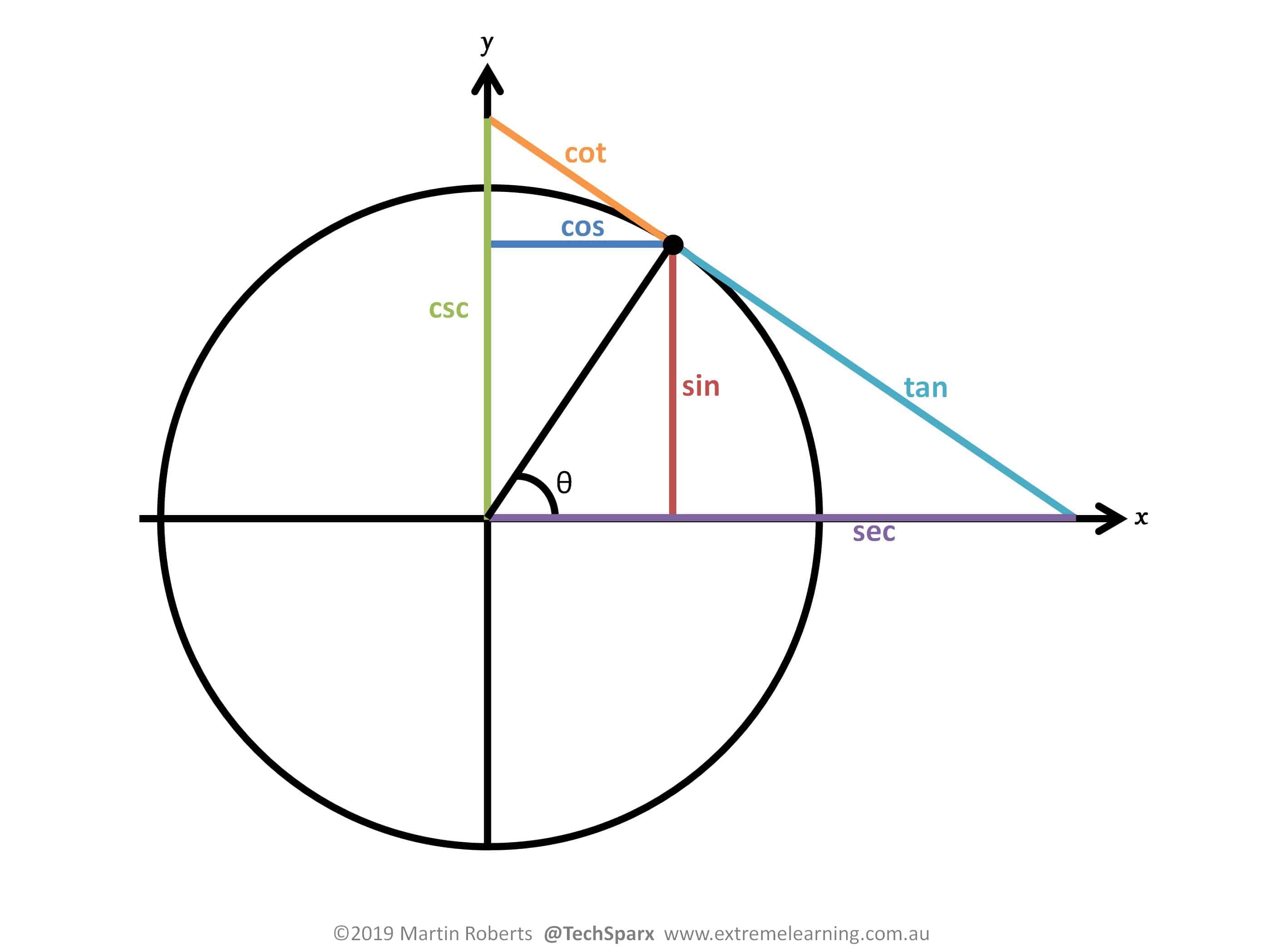
Mapping the Fibonacci lattice (aka Golden Spiral, aka Fibonacci Sphere) onto the surface of a sphere is an extremely fast and effective approximate method to evenly distribute points on a sphere. I show how small modifications to the canonical implementation can result in notable improvements for nearest-neighbor measures.
For many Monte Carlo methods, such as those in graphical computing, it is critical to uniformly sample from $d$-dimensional spheres and balls. This post describes over twenty different methods to uniformly random sample from the (surface of) a $d$-dimensional sphere or the (interior of) a $d$-dimensional ball.
Continue reading “How to generate uniformly random points on n-spheres and in n-balls”
This post shows how the core trigonometric definitions, relations and addition theorems can be simply and intuitively visualized.
This fun post illustrates the phenomenon of multiple uncoupled pendulums whose periods are all rational multiples of each other.
This post illustrates and explains the beautiful Lissajous Curves – trajectories of points whose coordinates follow sinusoidal movements. A simple but timeless classic curve that has numerous applications as well as artistic elegance.
If you are given the initial terms of a sequence, then here is an insanely simple method to derive a general formula for the first N terms, as well as the sum of the first N terms of the sequence.
Continue reading “A simple formula for Sequences and Series”
Unlike for circles, there isn’t a simple exact closed formula for the perimeter of an ellipse. We compare several well-known approximations, and conclude that a formula discovered by Ramanujan is our favourite, due to its simplicity and extreme accuracy.
Continue reading “A Formula for the Perimeter of an Ellipse”