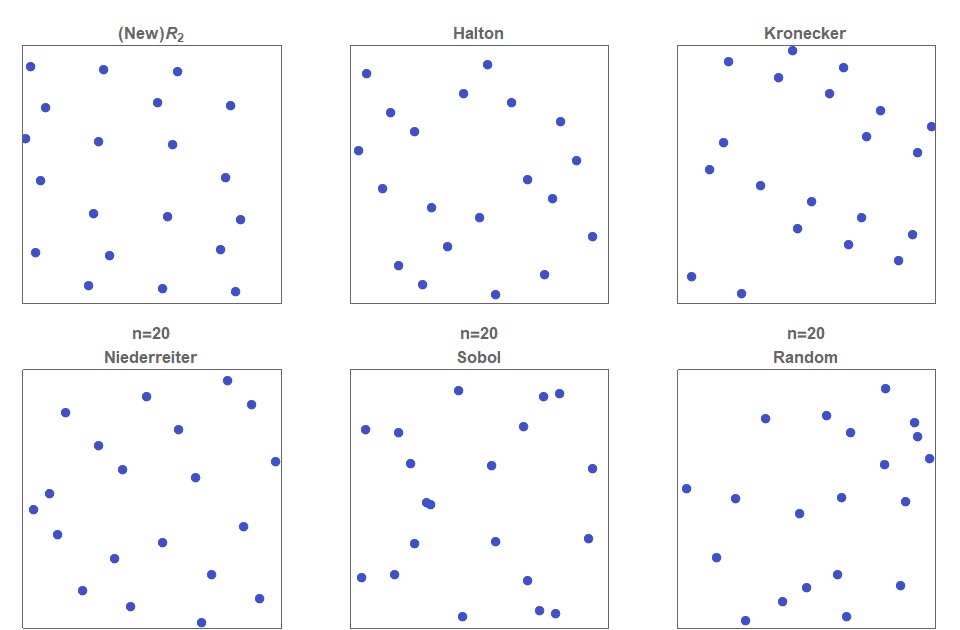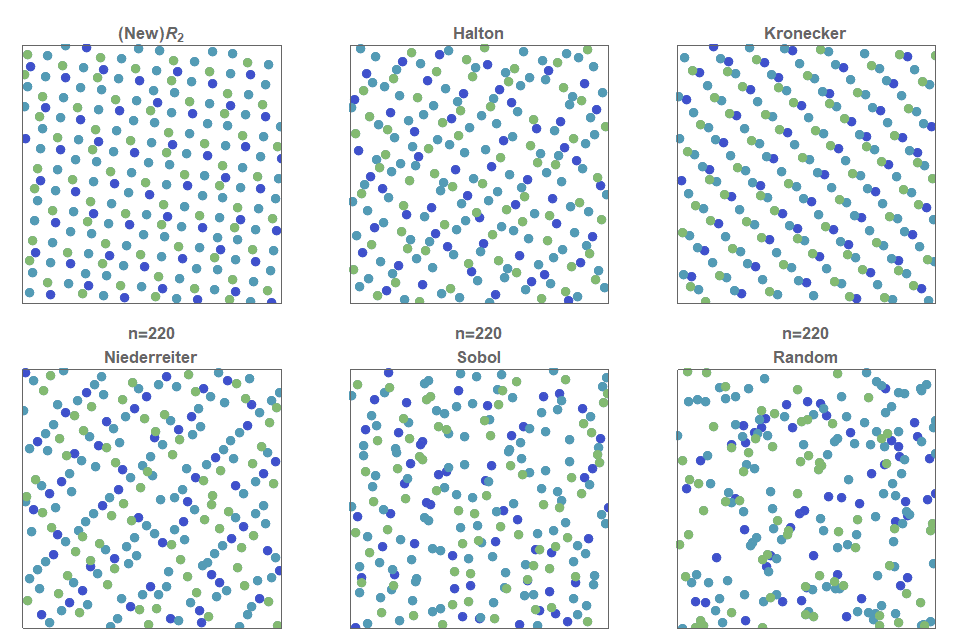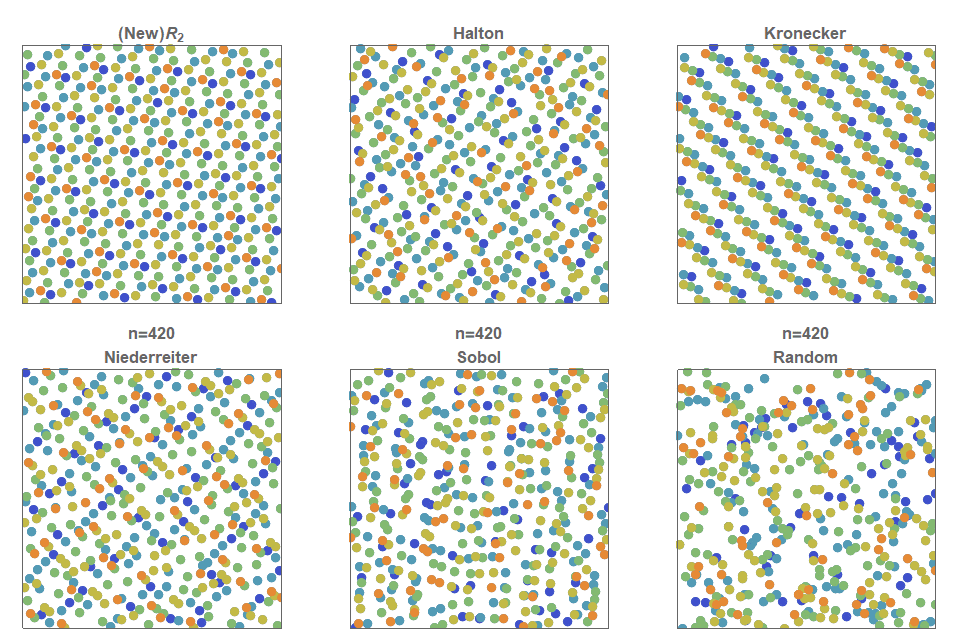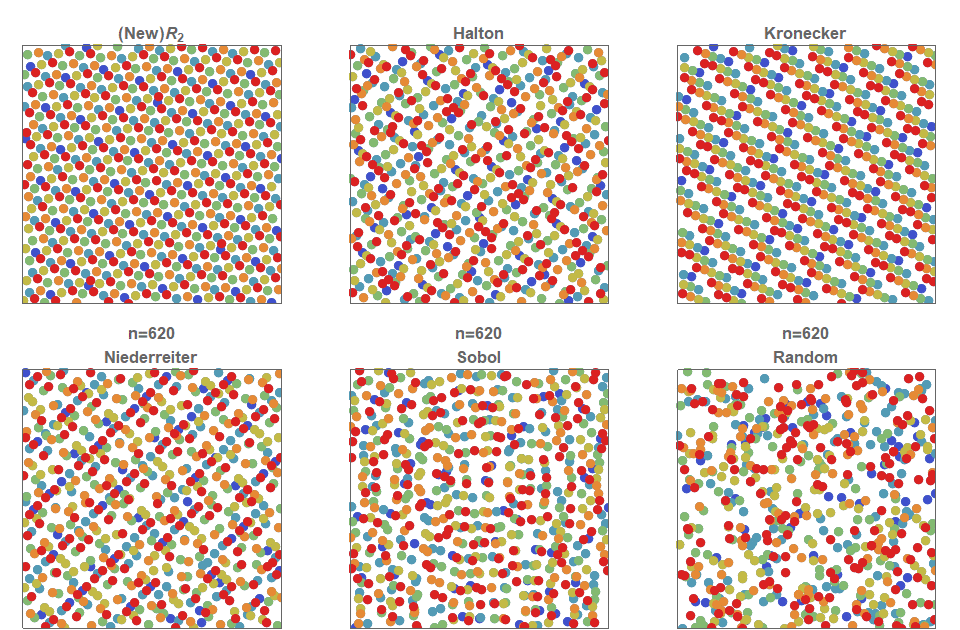
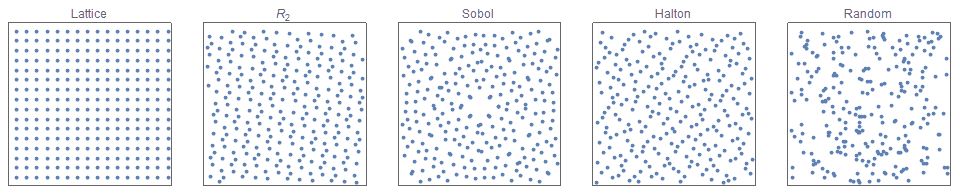
I present a new low discrepancy quasirandom sequence that offers many substantial improvements over other popular sequences such as the Sobol and Halton sequences.
Continue reading “The Unreasonable Effectiveness of Quasirandom Sequences”
Always curious. Always learning.
I present a new low discrepancy quasirandom sequence that offers many substantial improvements over other popular sequences such as the Sobol and Halton sequences.

Continue reading “The Unreasonable Effectiveness of Quasirandom Sequences”
I describe a probabilistic alternative to fractional factorial design based on the Sobol’ low discrepancy quasirandom sequence. This method is robust to aliasing (confounders), is often simpler to implement than traditional fractional factorial sample designs, and produces more accurate results than simple random sampling.
Continue reading “A probabilistic approach
to fractional factorial design”