I present a new low discrepancy quasirandom sequence that offers many substantial improvements over other popular sequences such as the Sobol and Halton sequences.
First published: 25th April, 2018
Last updated: 23 April, 2020
This blog post has been featured on the front page of Hacker News a few times (Aug 2018, Oct 2020 & April 2022). See here for the awesome discussion.
Topics Covered
- Low discrepancy sequences in one-dimension
- Low discrepancy methods in two dimensions
- Packing distance
- Multiclass low discrepancy sets
- Quasirandom sequences on the surface of sphere
- Quasiperiodic Tiling of the plane
- Dither masks in computer graphics
Introduction: Random versus Quasirandom
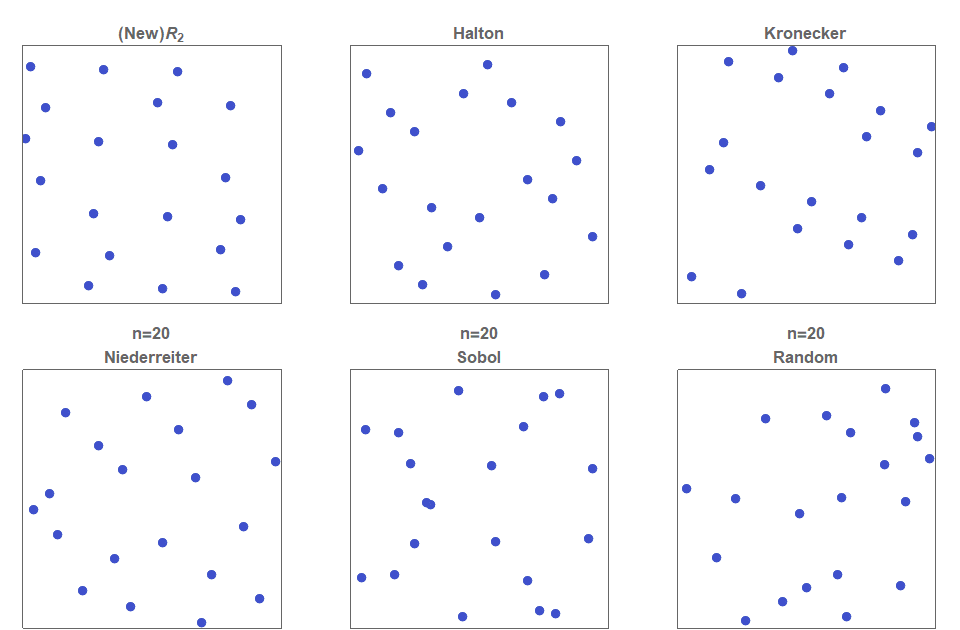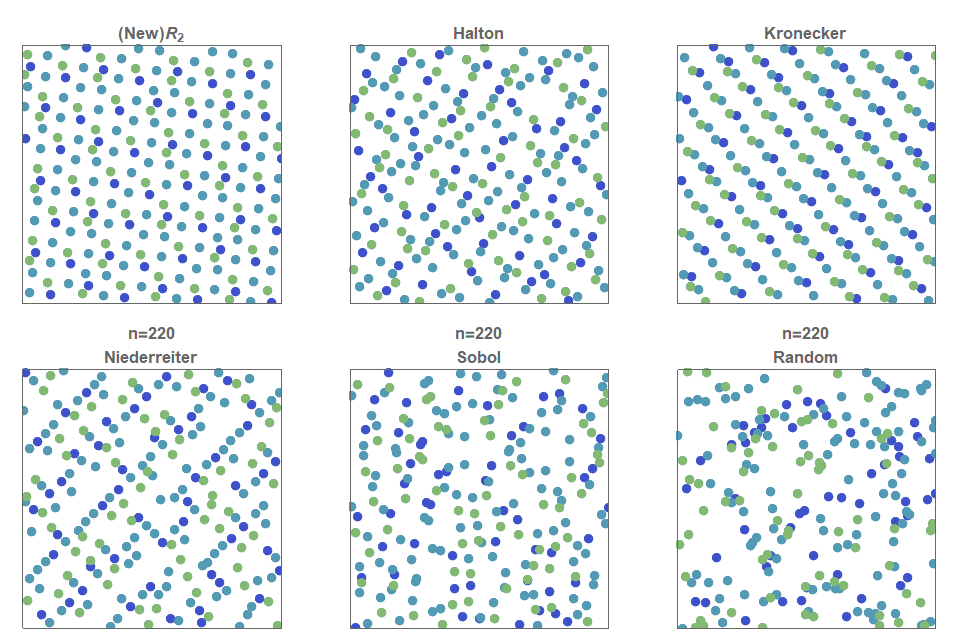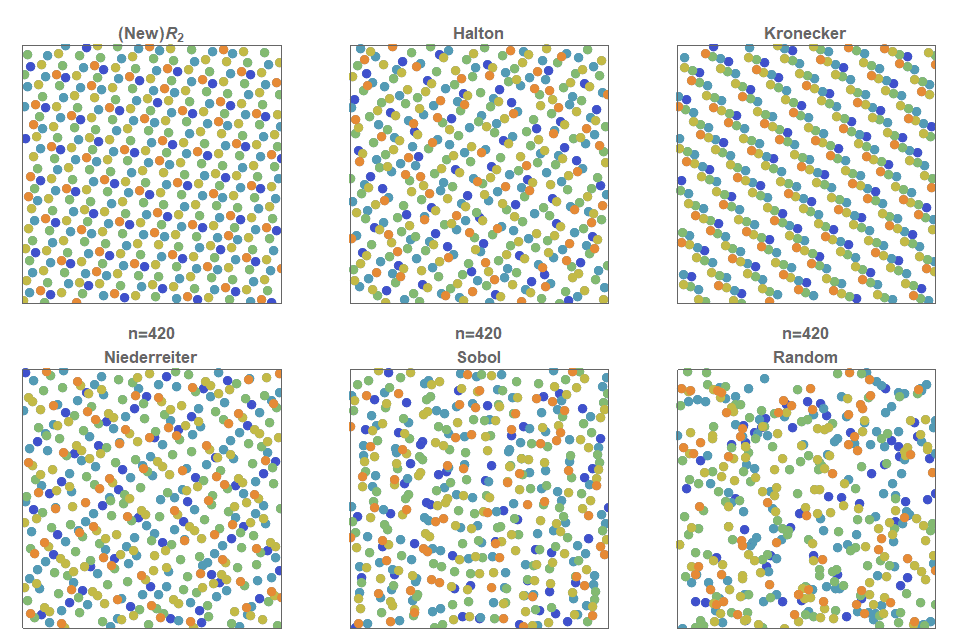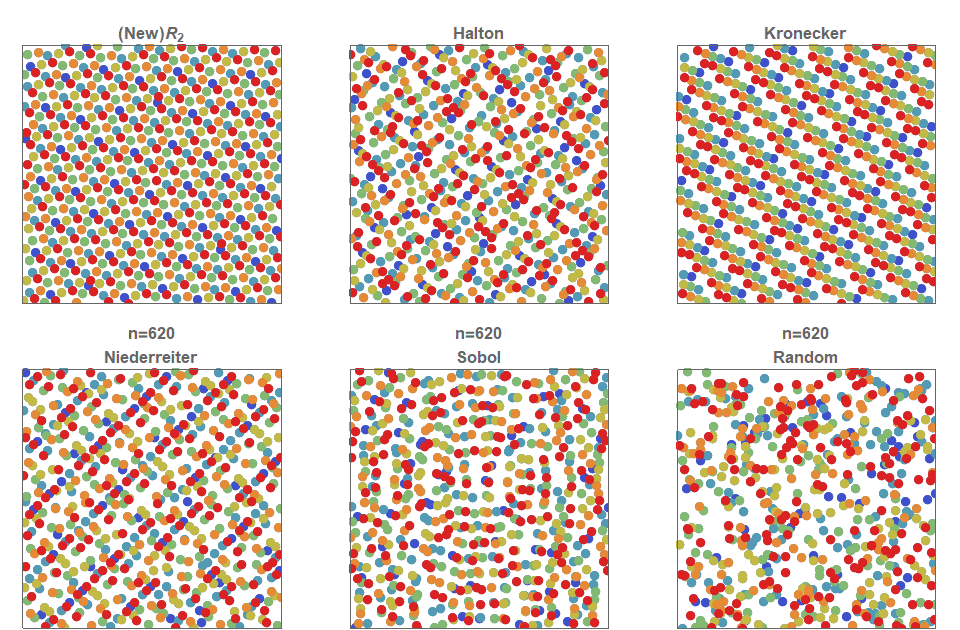
In figure 1b, it can be seen that the simple uniform random sampling of a point inside a unit square exhibits clustering of points, as well as regions that contain no points at all . A low discrepancy quasirandom sequence is a fully deterministic sequence of points that covers the entire space as uniformly as possible. They appear less regular than lattices but look more regular than random sampling (see figure 1b).
Well known quasirandom sequences include the Halton and Sobol sequences. They play a large role in many numerical computing applications, including physics, finance and in more recent decades computer graphics.
Simple random sampling is often called ‘white noise’, and low discrepancy quasirandom sequences are often called ‘blue noise’ samples’ (although technically blue noise and low discrepancy are two similar but distinct concepts).

Quasirandom Sequences in 1-dimension
The methods for creating low discrepancy quasirandom sequences in one dimension are extremely well studied.
The fundamental advantage of open sequences (that is, extensible in $n$) is that if the resultant error based on a given (finite) number of terms is still too large, the sequence can be arbitrarily extended without discarding all the previously calculated points.
There are many methods to construct open sequences. One way to categorise the different types is by the method of constructing their basis (hyper)-parameters:
- irrational fractions: Kronecker, Richtmyer, Ramshaw, Weyl
- (co)prime numbers: Van der Corput, Halton, Faure
- Irreducible Polynomials : Niederreiter
- Primitive polynomials: Sobol’
This post describes a new additive recurrence $R$-sequence that falls in the first category of those sequences that are based on specially chosen irrational numbers. We compare its properties with the Halton sequence and the Sobol sequence.
This special recurrence sequence is defined as: $$R_1(\alpha): \;\; t_n = \{s_0 + n \alpha\}, \quad n=1,2,3,…$$ where $\alpha $ is any irrational number. Note that the notation $ \{x\}$ indicates the fractional part of $x$. In computing, this function is more commonly expressed in the following way $$R_1(\alpha): \;\; t_n = s_0 + n \alpha \; (\textrm{mod} \; 1); \quad n=1,2,3,…$$ For $s_0 = 0$, the first few terms of the sequence, $R(\phi)$ are: $$t_n = 0.618, \; 0.236, \; 0.854, \; 0.472, \; 0.090, \; 0.708, \; 0.327, \; 0.944, \; 0.562, \; 0.180,\; 798,\; 416, \; 0.034, \; 0.652, \; 0.271, \; 0.888,…$$
It is important to note that the value of $s_0$ does not affect the overall characteristics of the sequence, and in nearly all cases is set to zero. However, especially in computing the option of $s \neq 0$ offers an additional degree of freedom that is often useful. Applying a non-zero value of $s$ is often called a toroidal shift, or a Cranley-Patterson transformation, and the resulting sequence is usually called a ‘shifted lattice sequence’.
The value of \( \alpha \) that gives the lowest possible discrepancy is achieved if \( \alpha = 1/\phi \), where \( \phi \) is the golden ratio. That is, $$ \phi \equiv \frac{\sqrt{5}+1}{2} \simeq 1.61803398875… ; $$ It is interesting to note that there are an infinite number of other values of $\alpha$ that also achieve optimal discrepancy, and they are all related via the Moebius transformation $$ \alpha’ = \frac{p\alpha+q}{r\alpha+s} \quad \textrm{for all integers} \; p,q,r,s \quad \textrm{such that} |ps-qr|=1 $$ We now compare this recurrence method to the well known van der Corput reverse-radix sequences [van der Corput, 1935] . The van der Corput sequences are actually a family of sequences, each defined by a unique hyper-parameter, b. The first few terms of the sequence for b=2 are: $$t_n^{[2]} = \frac{1}{2}, \frac{1}{4},\frac{3}{4}, \frac{1}{8}, \frac{5}{8}, \frac{3}{8}, \frac{7}{8}, \frac{1}{16},\frac{9}{16},\frac{5}{16},\frac{13}{16}, \frac{3}{16}, \frac{11}{16}, \frac{7}{16}, \frac{15}{16},…$$ The following section compares the general characteristics and effectiveness of each of these sequences. Consider the task of evaluating the definite integral $$ A = \int_0^1 f(x) \textrm{d}x $$ We may approximate this by: $$ A \simeq A_n = \frac{1}{n} \sum_{i=1}^{n} f(x_i), \quad x_i \in [0,1] $$
- If the \( \{x_i\} \) are equal to \(i/n\), this is the rectangle rule;
- If the \( \{x_i\} \) are chosen randomly, this is the Monte Carlo method; and
- If the \( \{x_i\} \) are elements of a low discrepancy sequence, this is the quasi-Monte Carlo method.
The following graph shows the typical error curves \( s_n = |A-A_n| \) for approximating a definite integral associated with the function, \( f(x) = \textrm{exp}(\frac{-x^2}{2}), \; x \in [0,1] \) with: (i) quasi-random points based on the additive recurrence, where \( \alpha = 1/\phi \), (blue); (ii) quasi-random points based on the van der Corput sequence, (orange); (iii) randomly selected points, (green); (iv) Sobol sequence (red). It shows that for \(n=10^6\) points, the random sampling approach results in an error of \( \simeq 10^{-4}\), the van der Corput sequence results in an error of \( \simeq 10^{-6}\), whilst the \(R(\phi)\)-sequence results in an error of \( \simeq 10^{-7}\), which is \(\sim\)10x better than the van der Corput error and \(\sim\) 1000x better than (uniform) random sampling.

Several things from this figure are worth noting:
- it is consistent with the knowledge that the errors based on uniform random sampling asymptotically decrease by $ 1/\sqrt{n} $, whereas error curves based on both quasi-random sequences tend to $1/n $.
- The results for the $R_1(\phi)$-sequence (blue) and Sobol (red) are the best.
- It shows that the van der Corput sequence produces error rates that are far better than random, but consistently not quite as good as Sobol or the new $R_1$ sequence.
The new $R_1$ sequence, which is a Kronecker sequence using the Golden ratio, is one of the best choices for one-dimensional Quasirandom Monte Carlo (QMC) integration methods
It should also be noted that although \(\alpha = \phi\) theoretically offers the provably optimal option, \(\sqrt{2}\) and is very close to optimal, and almost any other irrational value of \(\alpha\) provides excellent error curves for one-dimensional integration. This is why, \(\alpha = \sqrt{p} \) for any prime is very commonly used. Furthermore, from a computing perspective, selecting a random value in the interval $ \alpha \in [0,1] $ is with almost certainty going to be (within machine precision) an irrational number, and therefore a solid choice for a low discrepancy sequence. For visual clarity, the above figure does not show the results the Niederreiter sequence as the results are virtually indistinguishable to that of the the Sobol and $R$ sequences. The Neiderreiter and Sobol sequences (along with their optimized parameter selection) that were used in this post were calculated via Mathematica using what is documented as “closed, proprietary and fully optimized generators provided in Intel’s MKL library”.
Quasirandom sequences in two dimensions
Most current methods to construct higher dimension low discrepancy simply combine (in a component-wise manner), \(d\) one-dimensional sequences together. For brevity, this post mainly focuses on describing the Halton sequence [Halton, 1960] , Sobol sequence and the \(d-\)dimensional Kronecker sequence.
The Halton sequence is constructed simply by using \(d\) different one-dimensional van de Corput sequence each with a base that is relatively prime to all the others. That is, pairwise co-prime. By far, the most frequent selection, due to its obvious simplicity and sensibility, is to select the first \(d\) primes. The distribution of the first 625 points defined by the (2,3)-Halton sequence is show in figure 1. Although many two-dimensional Halton sequences are excellent sources for low discrepancy sequences, it is also well known that many are highly problematic and do not exhibit low discrepancies. For example, figure 3 shows that the (11,13)-Halton sequence produces highly visible lines. Much effort has gone into methods of selecting which pairs of ( \(p_1, p_2) \) are exemplars and which ones are problematic. This issue is even more problematic in higher dimensions.
Kronecker recurrence methods generally suffer even greater challenges when generalizing to higher dimensions. That is, although using \( \alpha = \sqrt{p} \) produces excellent one-dimensional sequences, it is very challenging to even find pairs of prime numbers to be used as the basis for the two dimensional case that are not problematic! As a way around this, some have suggested using other well-known irrational numbers, such as the \( \phi,\pi,e, … \). These produce moderately acceptable solutions but not are generally not used as they are usually not as good as a well-chosen Halton sequence. A great deal of effort has focused on these issues of degeneracy.
Proposed solutions include skipping/burning, leaping/thinning. And for finite sequences scrambling is another technique that is frequently used to overcome this problem. Scrambling can not be used to create an open (infinite) low discrepancy sequence.

Similarly, despite the generally better performance of the Sobol sequence, its complexity and more importantly the requirement of very careful choices of its hyperparameters makes it not as inviting.
- Thus reiterating, in $d$-dimensions:
- the typical Kronecker sequences require the selection of $d$ linearly independent irrational numbers;
- the Halton sequence requires $d$ pairwise coprime integers; and
- the Sobol sequence requires selecting $d$ direction numbers.
The new $R_d$ sequence is the only $d$-dimensional low discrepancy quasirandom sequence that does not require any selection of basis parameters.
Generalizing the Golden Ratio
tl;dr In this section, I show how to construct a new class of \(d-\)dimensional open (infinite) low discrepancy sequence that do not require choosing any basis parameters, and which has outstanding low discrepancy properties.
There are many possible ways to generalize the Fibonacci sequence and/or the Golden ratio. The following proposed method of generalizing the golden ratio is not new [Krcadinac, 2005]. Also the characteristic polynomial is related to many fields of algebra, including Perron Numbers, and Pisot-Vijayaraghavan numbers. However, what is new is the explicit connection between this generalized form and the construction of higher-dimensional low discrepancy sequences. We define the generalized version of the golden ratio,\( \phi_d\) as the unique positive root $ x^{d+1}=x+1 $. That is,
For \(d=1\), \( \phi_1 = 1.6180339887498948482… \), which is the canonical golden ratio.
For \(d=2\), \( \phi_2 = 1.324717957244746… \), which is often called the plastic constant, and has some beautiful properties (see also here). This value was conjectured to most likely be the optimal value for a related two-dimensional problem [Hensley, 2002].
For \(d=3\), \( \phi_3 = 1.22074408460575947536… \),
For $ d>3$, although the roots of this equation do not have a closed algebraic form, we can easily obtain a numerical approximation either through standard means such as Newton-Rhapson, or by noting that for the following sequence, \( R_d(\phi_d) \): $$ t_0=t_1 = … = t_{d} = 1;$$ $$t_{n+d+1} \;=\;t_{n+1}+t_n, \quad \textrm{for} \; n=1,2,3,..$$
This special sequence of constants, $\phi_d$ were called ‘Harmonious numbers‘ by architect and monk, Hans van de Laan in 1928. These special values can be expressed very elegantly as follows:
$$ \phi_1 = \sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+…}}}}} $$
$$ \phi_2 = \sqrt[3]{1+\sqrt[3]{1+\sqrt[3]{1+\sqrt[3]{1+\sqrt[3]{1+…}}}}} $$
$$ \phi_3 = \sqrt[4]{1+\sqrt[4]{1+\sqrt[4]{1+\sqrt[4]{1+\sqrt[4]{1+…}}}}} $$
We also have the following very elegant property: $$ \phi_d =\lim_{n\to \infty} \;\;\frac{t_{n+1}}{t_n} .$$ This sequence, sometimes called the generalized or delayed Fibonacci sequence, has been studied quite widely, [Kak 2004, Wilson 1993] and the sequence for \(d=2\) is often called the Padovan sequence [Stewart, 1996, OEIS A000931], whilst the \(d=3\) sequence is listed in [OEIS A079398]. As mentioned before, the key contribution of this post is to describe the explicit connection between this generalized sequence and the construction of \(d-\)dimensional low-discrepancy sequences.
Major Result: The following parameter-free \(d-\)dimensional open (infinite) sequence \(R_d(\phi_d)\), has excellent low discrepancy characteristics when compared to other existing methods. $$ \mathbf{t}_n = \{n \pmb{\alpha} \}, \quad n=1,2,3,… $$ $$ \textrm{where} \quad \pmb{\alpha} =(\frac{1}{\phi_d}, \frac{1}{\phi_d^2},\frac{1}{\phi_d^3},…\frac{1}{\phi_d^d}), $$ $$ \textrm{and} \; \phi_d\ \textrm{is the unique positive root of } x^{d+1}=x+1. $$
For two dimensions, this generalized sequence for \(n=150\), is shown in figure 1. The points are clearly more evenly distributed for the \(R_2\)-sequence compared to the (2, 3)-Halton sequence, the Kronecker sequence based on \( (\sqrt{3},\sqrt{7}) \), the Niederreiter and Sobol sequences. (Due to the complexity of the Niederreiter and Sobol sequences they were calculated via Mathematica using proprietary code supplied by Intel.) This type of sequence, where the basis vector $ \pmb{\alpha} $ is a function of a single real value, is often called a Korobov sequence [Korobov 1959]
See figure 1 again for a comparison between various 2-dimensional low discrepancy quasirandom sequences.
Code and Demonstrations
In summary in 1 dimension, the pseudo-code for the $n$-th term ($n$ = 1,2,3,….) is defined as
g = 1.6180339887498948482
a1 = 1.0/g
x[n] = (0.5+a1*n) %1
In 2 dimensions, the pseudo-code for the $x$ and $y$ coordinates of the $n$-th term ($n$ = 1,2,3,….) are defined as
g = 1.32471795724474602596
a1 = 1.0/g
a2 = 1.0/(g*g)
x[n] = (0.5+a1*n) %1
y[n] = (0.5+a2*n) %1
The pseudo-code for 3 dimensions, $x$, $y$ and $z$ coordinates of the $n$-th term ($n$ = 1,2,3,….) are defined as
g = 1.22074408460575947536
a1 = 1.0/g
a2 = 1.0/(g*g)
a3 = 1.0/(g*g*g)
x[n] = (0.5+a1*n) %1
y[n] = (0.5+a2*n) %1
z[n] = (0.5+a3*n) %1
Template python code. (Note that Python arrays and loops start at zero!)
import numpy as np
# Using the above nested radical formula for g=phi_d
# or you could just hard-code it.
# phi(1) = 1.6180339887498948482
# phi(2) = 1.32471795724474602596
def phi(d):
x=2.0000
for i in range(10):
x = pow(1+x,1/(d+1))
return x
# Number of dimensions.
d=2
# number of required points
n=50
g = phi(d)
alpha = np.zeros(d)
for j in range(d):
alpha[j] = pow(1/g,j+1) \% 1
z = np.zeros((n, d))
# This number can be any real number.
# Common default setting is typically seed=0
# But seed = 0.5 might be marginally better.
for i in range(n):
z[i] = (seed + alpha*(i+1)) %1
print(z)
I have written the code like this to be consistent with the maths conventions used throughout this post. However, for reasons of programming convention and/or efficiency there are some modifications worth considering. Firstly, as $R_2$ is an additive recurrence sequence, an alternative formulation of $z$ which does not require floating point multiplication and maintains higher levels of accuracy for very large $n$ is
z[i+1] = (z[i]+alpha) %1 Secondly, for those languages that allow vectorization, the fractional function code could be vectorised as follows:
for i in range(n):
z[i] = seed + alpha*(i+1)
z = z %1
Finally, you could replace this floating point additions with integer additions by multiplying all constants by $2^{32}$, and then modifying the frac(.) function accordingly. Here are some demonstrations with included code, by other people based on this sequence:
- beta.observablehq.com/@jrus/plastic-sequence by Jacob Rus:
- www.shadertoy.com/view/4dtBWH by @Stirners Chost (XGKICK):
Minimum Packing Distance
The new $R_2$-sequence is the only 2-dimensional low discrepancy quasirandom sequence where the minimum packing distance falls only by $1/\sqrt{n}$.
Although any of the quasirandom sequences can be used for integration (where $R_d$ or the Sobol sequence are excellent choices) it seems the defining difference between $R_d$ and Sobol is that $R_d$ optimizes for packing distance.
Although the standard technical analysis of quantifying discrepancy is by analysing the \(d^*\)-discrepancy, we first mention a couple of other geometric (and possibly more intuitive ways!) of how this new sequence is preferable to other standard methods. If we denote the distance between points \(i\) and \(j\) to be \(d_{ij}\), and \(d_0 = \textrm{inf} \; d_{ij} \), then the following graph shows how \(d_0(n)\) varies for the \(R\)-sequence, the (2,3)-Halton, Sobol, Niederrieter and the random sequences. This can be seen in the following figure 6.
Like the previous figure, each minimum distance measure is normalized by a factor of \( 1/\sqrt{n} \). One can see that after \(n=300\) points, it is almost certain that for the random distribution (green) there will be two points that are extremely close to each other. It can also be seen that although the (2,3)-Halton sequence (orange) is much better than the random sampling, it also unfortunately asymptotically goes to zero. The reason why the normalized $d_0$ goes to zero for the Sobol sequence is because Sobol himself showed that the Sobol sequence falls at a rate of $1/n$ — which is good, but obviously much worse than for $R_2$ which only falls by $1/\sqrt{n}$.
For the \(R(\phi_2)\) sequence, (blue), the minimum distance between two points consistently falls between $0.549/\sqrt{n} $ and $0.868/\sqrt{n} $. Note that the optimal diameter of 0.868 corresponds to a packing fraction of 59.2%. Compare this to other circle packings.
Also note that the Bridson Poisson disc sampling which is not extensible in \(n\), and on typical recommended setting, still only produces a packing fraction of 49.4%. Note that this concept of \(d_0\) intimately connects the \( \phi_d \) low discrepancy sequences with badly approximable numbers/vectors in \(d\)-dimensions [Hensley, 2001]. Although a little is known about badly approximable numbers in two dimensions, the construction of \(phi_d\) might offer a new window of research for higher badly approximable numbers in higher dimensions.

Voronoi Diagrams
Another method of visualizing the evenness of a point distribution is to create a Voronoi diagram based on the first \(n\) points of a 2-dimensional sequence, and then color each region based on its area. In the figure below, shows the color-based Voronoi diagrams for (i) the $R_2$-sequence; (ii) the (2,3)-Halton sequence, (iii) prime-based recurrence; and (iv) the simple random sampling; . The same color scale is used for all figures. Once again, it is clear that the $R_2$-sequence offers a far more even distribution than the Halton or simple random sampling. This is the same as above, but colored according the the number of vertices of each voronoi cell. Not only is it clear that the \(R\)-sequence offers a far more even distribution than the Halton or simple random sampling, but what is more striking is that for key values of $n$ it only consists of hexagons! If we consider the generalised Fibonacci sequence, $A_1=A_2=A_3=1; \quad A_{n+3} = A_{n+1}+A{n}$. That is, $A_n:$, \begin{array}{r} 1& 1& 1& 2& 2& 3& 4& 5& 7\\ 9& \textbf{12}& 16& 21& 28& 37& \textbf{49}& 65& 86\\ 114& \textbf{151}& 200& 265& 351& 465& \textbf{616}& 816& 1081 \\ 1432& \textbf{1897}& 2513& 3329& 4410& 5842& \textbf{7739}& 10252& 13581\\ 17991& \textbf{23833}& 31572& 41824& 55405& 73396& \textbf{97229}& 128801& 170625\\ 226030& \textbf{299426}& 396655& 525456& 696081& 922111& \textbf{1221537}& 1618192& 2143648 \\ \end{array} All values where $n= A_{9k-2}$ or $n= A_{9k+2}$ will consist only of hexagons.

For particular values of $n$, the Voronoi mesh of the $R_2$ sequence consists only of hexagons.

Quasiperiodic Delaunay Tiling of the plane
The $R$-sequence is the only low discrepancy quasirandom sequence that can be used to produce $d$-dimensional quasiperiodic tilings through its Delaunay mesh.
Delaunay Triangulation (sometimes spelt ‘Delone Triangulation’), which is the dual of the Voronoi graph, offers another way of viewing these distributions. More importantly, though, Delaunay triangulation, offers a new method of creating quasiperiodic tilings of the plane. Delaunay triangulation of the $R_2$-sequence offer a far more regular pattern than that of the Halton or Random sequences,. More specifically, the Delaunay triangulations of point distributions where $n$ is equal to any of the generalised Fibonacci sequence $:A_N=$ 1,1,1,2,3,4,5,7,9,12,16,21,28,37,… then the Delaunay triangulation consists of of only 3 identically paired triangles, that is, parallelograms (rhomboids)! (excepting those triangles that have a vertex in common with the convex hull.) Furthermore,
For values of $n=A_k$, the Delaunay triangulation of the $R_2$-sequence form quasiperiodic tilings that each consist only of three base triangles (red, yellow, blue) which are always paired to form a well-defined quasiperiodic tiling of the plane via three parallelograms (rhomboids).

Note that $R_2$ is based on $\phi_2=1.32471795724474602596$ is the smallest Pisot number, (and $\phi = 1.61803…$ is the largest Pisot number. The association of quasiperiodic tilings with quadratic and cubic Pisot numbers is not new [Elkharrat and also Masakova] , but I believe that this is the first time a quasiperiodic tiling has been constructed based on $\phi_2$ =1.324719….
(Note: a post titled “Shattering the plane with twelve new Substitution Tilings” [Pegg Jr., 2019] is most likely related to this $R_2$ tiling, but I will probably need a separate post to explore the possible connections.)
This animation below shows how the Delaunay mesh of the $R_2$ sequence changes as points are successively added. Note that whenever the number of points is equal to a term in the generalised Fibonacci sequence, then the entire Delaunay mesh consists only of red, blue and yellow parallelograms (rhomboids) arranged in a 2-fold quasiperiodic manner.
Figure 7.
Although the locations of red parallelograms show considerable regularity, one can clearly see that the blue and yellow parallelograms are spaced in a quasiperiodic manner. The fourier spectrum of this lattice can be seen in figure 11, and shows the classic point-based spectra. (Note that the prime-based recurrence sequence also appears quasiperiodic in the weak sense that it is an ordered pattern that is not repeating. However, its pattern over a range of $n$ is not so consistent and also critically dependent on the selection of basis parameters. For this reason, we focus our interest of quasiperiodic tilings solely on the $R_2$ sequence.) It consists of only three triangles: red, yellow, blue. Note that for this R(\(\phi_2)\) sequence, all the parallelograms of each color are exactly the same size and shape. The ratio of the areas of these individual triangles is extremely elegant. Namely, $$ \textrm{Area(red) : Area(yellow) : Area(blue) }= 1 : \phi_2 : \phi_2^2 $$ And so is the relative frequency of the triangles, which is: $$ f(\textrm{red}) : f(\textrm{yellow}) : f(\textrm{blue}) = 1 : \phi_2 : 1 $$ From this, it follows that the total relative area covered in space by these three triangles is: $$ f(\textrm{red}) : f(\textrm{yellow}) : f(\textrm{blue}) = 1 : \phi_2^2 : \phi_2^2$$ One would also presume that we could also create this quasiperiodic tiling through a substitution based on the A sequence. That is, $$ A \rightarrow B; \quad B \rightarrow C; \quad C \rightarrow BA $$. For three dimensions, if we consider the generalised Fibonacci sequence, $B_1=B_2=B_3=B_4=1; \quad B_{n+4} = B_{n+1}+B{n}$. That is, $$ B_n = \{ 1,1,1,1,2,2,2,3,4,4,5,7,8,9,12,15,17,21,27,32,38,48,59,70,86,107,129,… \}
For particular values of $n=B_k$, the 3D-Delaunay mesh associated with the $R_3$-sequence defines a quasiperiodic crystal lattice.
Discretised Packing. part 2
In the following figure, the first \(n=2500\) points for each two-dimensional low discrepancy sequence are shown. Furthermore, each of the 50×50=2500 cells are colored green only if that cell contains exactly 1 point. That is, more green squares indicates a more even distribution of the 2500 points across the 2500 cells. The percentage of green cells for each of these figures is: \(R_2\) (75%), Halton (54%), Kronecker (48%), Neiderreiter (54%), Sobol (49%) and Random (38%). ![]()
Multiclass Low Discrepancy sets
Some of the low discrepancy sequences exhibit what called be termed ‘multiclass low discrepancy’. So far we have assumed that when we need to distribute $n$ points as evenly as possible that all the points are identical and indistinguishable. However, in many situations there are different types of points. Consider the problem of evenly distributing the $n$ points so that not only are all the points evenly separated, but also all points of the same class are evenly distributed. Specifically, suppose that if there are $n_k$ points of type $k$, (where $n_1+n_2+n_3 +… +n_k= n$) , then a multiset low discrepancy distribution is where each of the $n_k$ points are evenly distributed In this case, we find that the $R$-sequence and the Halton sequence can be easily adapted to become multiset low discrepancy sequences, simply allocating consecutively allocating the points of each type.
The figure below shows how $n=150$ points have been distributed such that 75 are blue, 40 green 25 green and 10 red. For the additive recurrence sequence this is trivially achieved by simply setting the first 75 terms to correspond to blue, the next 40 to orange, the next 25 to green and the last 10 to red. This technique works almost works for the Halton and Kronecker sequences but fares very poorly for Niederreiter and Sobol sequences. Furthermore, there are no known techniques for consistently generating multiscale point distributions for Niederreiter or Sobol sequences. This shows that multiclass point distributions such as those in the eyes of chickens, can now be described and constructed directly via low discrepancy sequences.
The $R_2$ sequence is a low discrepancy quasirandom sequence that admits a simple construction of multiclass low discrepancy.

Quasirandom Points on a sphere
It is very common in the fields of computer graphics and physics to need to distribute points on the surface of a 2-sphere as evenly as possible. Using open (infinite) quasi-random sequences, this task merely mapping (lifting) the quasi-random points that are distributed evenly in the unit square onto the surface of a sphere via a Lambert equal-area projection. The standard Lambert projection transformation that maps a point \( (u,v) \in U[0,1] \to (x,y,z)\in S^2\), is : $$ (x,y,z) = (\cos \lambda \cos \phi, \cos \lambda \sin \phi, \sin \lambda), $$ $$ \textrm{where} \quad \cos (\lambda -\pi/2) = (2u-1); \quad \phi = 2\pi v. $$ As this \(\phi_2-\)squence is fully open, it allows you to map an infinite sequence of points onto the surface of a sphere – one point at a time. This is in contrast to other existing methods such as the Fibonacci spiral lattice which requires knowing in advance, the number of points. Once again, through visual inspection, we can clearly see that for \(n=1200\), the new \(R(\phi_2)\)-sequence is far more even than the Halton mapping or Kronecker sampling which in turn is far more even than random sampling.

Dithering in computer graphics
Most state-of-the-art dithering techniques (such as those based on Floyd-Steinberg) are based on error-diffusion, which are not well suited for parallel processing and/or direct GPU optimisation. In these instances, point-based dithering with static dither masks (ie fully independent of the target image) offer excellent performance characteristics. Possibly the most famous, and still widely used dither masks are based on Bayer matrices, however, newer ones attempt to more directly mimic blue noise characteristics. The non-trivial challenge with creating dither masks based on low discrepancy sequences and/or blue noise, is that these are low discrepancy sequences map an integer \(Z\) to a two-dimensional point in the interval \( [0,1)^2 \). In contrast, a dither mask requires a function that maps two-dimensional integer coordinates of the rastered mask to a real valued intensity/threshold in the interval \( [0,1) \).
I propose the following approach which is based on the $R$-sequence. For each pixel (x,y) in the mask, we set its intensity to be \(I(x,y) \), where: $$ I(x,y) = \alpha_1 x + \alpha_2 y \; ( \textrm{mod} 1); $$ $$ \textrm{where} \quad \pmb{\alpha} =(\alpha_1,\alpha_2) = (\frac{1}{\phi_2}, \frac{1}{\phi_2^2}), $$ $$ \textrm{and} \; \phi_2\ \textrm{is the unique positive root of } x^3\;=x+1.$$ That is, $x = 1.324717957…$, and thus $$\alpha_1 = 0.7548776662; \alpha_2 = 0.56984029$$ Furthermore, if an additional triangular wave function is included in order to eliminate the discontinuity caused by the frac(.) function at each integer boundary: $$ T(z) =\begin{cases} 2z, & \text{if } 0\leq z <1/2 \\ 2-2z, & \text{if} 1/2 \leq z < 1 \end{cases} $$ $$ I(x,y) = T \left[ \alpha_1 x + \alpha_2 y \; ( \textrm{mod} 1) \right]; $$ the mask and its fourier/periodogram are even further improved. Also, we note that because $$ \lim_{n \rightarrow \infty} \frac{A_n}{A_{n+1}} = 0.754878 ; \quad \lim_{n \rightarrow \infty} \frac{A_n}{A_{n+2}} = 0.56984 $$ The form of the above expression is related to the following linear congruential equation $$ A_n x + A_{n+1} y \; (\textrm{mod} A_{n+2}) \textrm{ for integers } \;\; x,y$$
The R-dither masks produce results that are competitive with state-of-the-art methods blue noise masks. But unlike blue noise masks, they do not need to be pre-computed, as they can be calculated in real-time.
Note that this structure has also been suggested by Mittring but he finds the coefficients empirically (and does not quote the final values). Furthermore, it assists in understanding why the empirical formula by Jorge Jimenez when making “Call of Duty”, often termed “Interleaved Gradient Noise” works so well. $$I(x,y) = (\textrm{FractionalPart}[52.9829189*\textrm{FractionalPart}[0.06711056*x + 0.00583715*y]] $$ However, this required 3 floating point multiplications and two %1 operators, whereas the prior formula shows that we can do it with just 2 floating point multiplications and a single %1 operation. More importantly, this post gives a firmer math understanding as to why a dither mask of this form is so effective, if not optimal. The results of this dither matrix are shown below for the classic 256×256 “Lena” test image, as well as a checkered test pattern. The results using the standard Bayer dither masks is also shown, as well as one based on blue noise. The two most common methods for blue noise is Void-and-Cluster and Poisson disc sampling. For brevity I have only included results using the Void and cluster method. [Peters]. The interleaved gradient noise works better than Bayer and blue noise, but not quite as good as the $R$-dither. One can see that the Bayer dither exhibits noticeable white dissonance in the light gray areas. The $R$-sequence and blue noise dither are generally comparable though slight differences can be discerned. A few things to note about the R-dither:
- It is not isotropic! The Fourier spectra shows only distinct and discrete points. This is the classic signature of quaisperiodic tilings and diffraction spectra of quaiscrystals. Specifically, the Fourier spectra of the $R$-mask is consistent with the fact that the The R-sequence is a linear recurrence.
- The R-dither when combined with a triangular wave produces an incredibly uniform mask!
- despite the differing visual appearances of the two R-dither masks, there is almost no difference in final dithered results.
- Looking at Lena’s lips and shoulders, one might argue that the R-dither produces clearer results than the blue noise mask. This is even more noticeable when using 512×512 dithering matrices (but not shown).
- The intensity $(I(x,y)$ is intrinsically a real-valued number and so the masks naturally scales to arbitrary bit-depths.


Higher Dimensions
Similar to the prior section, but for five (5) dimensions, the graph below shows the (global) minimum distance between any two points, for the \( R(\phi_5)\)-sequence, the (2,3,5,7,11)-Halton and the random sequences. This time, the normalized minimum distance measure is normalized by a factor of \( 1/ \sqrt[5]{n} \). One can see that, as a consequence of ‘the curse of dimensionality’, the random distribution is better than all the low discrepancy sequences — except the $R_5$-sequence. The \(R(\phi_5)\)-sequence , even for \( n \simeq 10^6\) points, the minimum distance between two points is still consistently around \( 0.8/\sqrt{n} \), and always above \( 0.631/\sqrt{n} \).
The $R_2$ sequence is the only $d$-dimensional low discrepancy sequence, where the packing distance only falls at a rate of $n^{-1/d}$.

Numerical Integration
The following graph shows the typical error curves \( s_n = |A-A_n| \) for approximating a definite integral associated with a Gaussian function of half-width \(\sigma = \sqrt{d}\), \( f(x) = \textrm{exp}(\frac{-x^2}{2d}), \; x \in [0,1] \), with: (i) \( R_{\phi} \) (blue); (ii) Halton sequence, (orange); (iii) randomly (green); (iv) Sobol (red) It shows that for \(n=10^6\) points, the differential between random sampling is the Halton sequence is somewhat less now. However, as was seen in the 1-dimensional case, the $R$-sequence and the Sobol are consistently better than the Halton sequence. It also suggests that the Sobol sequence is marginally better than the $R$-sequence.

***
My name is Dr Martin Roberts, and I’m a freelance Principal Data Science consultant, who loves working at the intersection of maths and computing.
“I transform and modernize organizations through innovative data strategies solutions.”You can contact me through any of these channels.
LinkedIn: https://www.linkedin.com/in/martinroberts/
Twitter: @TechSparx https://twitter.com/TechSparx
email: Martin (at) RobertsAnalytics (dot) com
More details about me can be found here.
Great investigation, I like it a lot. One comment from user side: In electrical engineering we often run MC, e.g. using 1000 points. However, the integral on f as Gaussian pdf is of very low interest, usually f is a simulation result which indeed might follow the normal pdf, BUT this integral would give the mean value. Engineers much more need to know the stddev (or even skew and kurtosis)! And here the sampling accuracy close to the corners is much more important compared to integration on uniform distribution or for integration to get the mean. I think the speed-up in 5D will be much lower for more difficult estimates like kurtosis or 4th moment of Gaussian distribution. Interestingly the QMC error is only weakly connected to discrepancy in this case, because all discrepancy measures change not much if extreme samples would be in your point set (like a 6-sigma outlier), but extreme samples could change e.g. kurtosis easily by 50%.
Hi Stephan,
Thanks for your comments, glad you liked it! You raise a really interesting point about k-moments, that was certainly not addressed in this post. My background is from maths/theoretical physics, so thanks for the engineering perspective. You have inspired me to do some further investigations into using this new sequence, and low-discrepancy sequences in general, for calculation of higher moments — so watch this space for a future blog post on this topic! Also related to you experiences, but not mentioned in this article is that I have found there is not always an obvious relationships between integration error and formal discrepancy measures. For example, my R(phi) sequence has an almost identical d-star discrepancy to the Halton sequences, and yet it consistently produces lower integration errors. It would be great to identify a formal discrepancy measure that reflects its effectiveness for the specific applications mentioned in this post, as well as applications (eg k-moments) that you mention.
Hi Robert, I made similar observations in discrepancy for your new sequences and Halton. One thing is that for moderate N like 500 to 1000 and d like 2 to 10 Halton works not soo bad, and with leaped Halton or Hammersley you can slightly improve. For all techniques and fix N also a latinization helps pretty much to reduce discrepancy further, BUT at d>10 the trouble begins fot almost all methods I know. The best point sets I know are collected under http://www.math.hkbu.edu.hk/UniformDesign. There, a large but still very good design is available for N=30 and d=10 – having CL2^2=0.066271. This is incredable good, and much better than Hammersley and all other methods I looked at so far (like Sobol, Niederreiter/Xing, Faure, etc.).
Bye Stephan
Hi again,
As you can see from the notes at the bottom of my post, I was going to explore using low discrepancy sequences as a probabilistic method of generalizing factorial methods. It seems that the reference you mention (which I had not see before, so thanks) describes a very similar idea.
Overall, my experience with my new R sequence is that it its main use is to add efficiency to methods where low discrepancy sequences have already shown their benefit. And that although there are improved and generalizations to the canonical low discrepancy sequences (such as what you mention) they tend to just be incremental engineered changes rather than deeply new methods. Furthermore, these evolutionary improvements typically come at the expense of added sequence construction and/or behaviour complexity. Thus I feel that the fields and engineering and physics where we need to do very high dimensional analysis will remain problematic.
However, I believe that there is one fascinating area where low discrepancy sequences can still shine and we have not fully explored its possibilities – and that is in problems that appear very high in dimensional, but the effective dimension of the problem space is much smaller and that the solutions represent an low-ish dimensional manifold embedded in a higher dimension. In these cases, low discrepancy sequences were dismissed (too?) quickly due to their theoretical (log N)^D convergence. It seems that many years ago, it was found that many of the integrals in finance were like this, and now we are learning that many of the problems in machine learning might also be similar.
Cheers! Martin Roberts
Hey there, this discovery made into a demoscene forum.
Please check my reply there, i found a really short way
to traverse a plain (fractal), where each pixel is visited
exactly ONCE in 2014, and made a demo about it 😉
https://www.pouet.net/topic.php?which=11501&page=1#c546333
Hi,
I am not quite sure what you mean exactly. Do you have a demo which might help me visualise it?
For example this tiny intro : https://www.pouet.net/prod.php?which=63522
I improved the version later to be “solid”, visiting every point of the fractal
exactly ONCE per cycle, allowing a smooth fake fading without mixing colors
or anything : https://www.youtube.com/watch?v=SImgzSNED84
that would indicate a complete green picture in the “covering” section of
your article, of course regarding the fractal and not the plane (you could
imagine fitting a plane into the fractal, or finding an IFS for a square)
As i wrote here http://www.pouet.net/topic.php?which=10164
(please forgive the unscientific notations there)
you can track the series of branches which were made to draw
the fractal (it’s 2 functions, applied in pseudorandom sequence)
and this binary series seems to be pretty random ( i once created
an image from it, and it showed absolutely no pattern in it)
Back then in 2014, i was pretty puzzled when i found that you
don’t need a GOOD random number generator to draw a
IFS fractal – you need NONE. I still have problems to exactly
formalize this, for example the shift of the domain from
continuous to discrete. It seems that the fractal and the
random number generator are heavily intertwined, or
even the same.
I hope i made myself a bit more clear. Again, i still don’t fully
understand how this is even possible 😉
Finding a method to attain complete coverage for an IFS is certainly very interesting. I will look at it more closely and get back to you if I learn anything!
Interesting work! I tried modifying your template code to show the two-dimensional projections of higher dimensions (https://github.com/anderslanglands/notebooks/blob/master/r2_sequence_01.ipynb) , and the results look quite bad, e.g.
(11, 13) – https://plot.ly/~anderslanglands/1/#/
(6, 15) – https://plot.ly/~anderslanglands/3/#/
Is this to be expected at low sample numbers?
Hi Anders,
Nice work! Your observations are consistent with what I have found so far from my brief explorations on projections of R_2 in higher dimensions. However, it is not an artefact of small numbers, as you will find the same phenomenon for large n. 🙁
And actually most of the standard low discrepancy sequences have some quite poor projections.
To be honest, I am not fully sure what to make of it, which is one reason didn’t mention it in my post yet.
On one hand, this is to be expected because unlike in Halton or Kronecker sequences where the basis numbers (eg primes) are chosen to be pairwise independent, the basis parameters for each dimensional coordinate of the R_2 sequences are all highly related as they are all powers of phi_D.
However, on the other hand it is therefore quite counter-intuitive (and thus definitely worth deeper investigation!) as to why holistically the R_D sequence in high dimensions work as effectively, if not better than Halton. For example, in high-dimensional integration.
A possible hint might lie in my sections on Minimal distance, Delaunay triangulation and Voronoi meshes. You can see that in 2 dimensions that the points of R_2 are a lot more regularly ‘evenly’ packed. That is, the points in R_2 approximate a hexagonal lattice better than any of the other sequences. This is why they get such a minimal distance measure and a very high circle packing ratio. Contrast this to the Sobol and Niederrieter sequences where there is no discernible pattern. This phenomenon also occurs in higher dimensions say R_3. So I guess if you are taking a 2-dimensional slice of a near optimal D-dimensional spherical packing you are almost certain to get a distinct pattern….
I am quickly learning that for all these low discrepancy sequences they all have their pros and cons, as they all have quite distinct characteristics and so are often optimal in different situations…
Hope that helps!
ps You may also like this paper on the projections of higher dimensional low discrepancy quasirandom sequences: https://www.sciencedirect.com/science/article/pii/S0377042707000374
I think it is to be expected that the incremental fill pattern will be more visible looking at subset of dimensions, as the space fill up with points evenly by virtue of each dimension ‘cycling’ to a different ‘beat’.
There seem to be some set sizes which complete the visitation through all dimensions best, and lesser sizes which leave regular sections of places visibly unvisited.
To get an even spread it would be optimal to set the size (n) in accordance with a cycles_complete size.
Or for a given n, calculate the next larger cycles-complete size, and step through i by cycles_complete/n.
Or just calculate the cycles_complete set and randomly knock points out till n is left.
I think patterns evenly spread through such cycles_complete size will be much more even looking even when isolating dimensions from others.
I am curious about how to calculate cycles_complete sizes.
Here is an image of 2 dimensions of R3 dimension fill: https://imgur.com/a/1r18Z3d
From a test page for a Javascript utility module which I have included these sequences of Martin Roberts in.
https://github.com/strainer/Fdrandom.js
Thankyou for this and such helpful articles. For example I appreciated this tip that the square brackets [x] mean, x modulo 1, sometimes in math script 🙂
Yes, I noticed also noticed that some values of n seem to offer more even distributions for their subset projections and so it would be interesting (even for d=2) to find which specific values are optimal.
Whoops! I am so embarrassed. I made a typo in my blog (now fixed). The math notation for the fractional part of x is $\{x\}$ and not $[x]$ as I originally wrote. That is, with curly brackets not square brackets. Square brackets usually denote the integer part of x.
Easy done with the brackets, thats the kind of tip I appreciate anyway.
I think set sizes of powers of 2 have a certain completedness in R2.
It seems after a power of 2 the range to the next power of two, fills in the biggest gap pattern left by the previous, as well as near missing much of the the previous pattern, and leaves a new biggest gap pattern for the next range to fit. Quite fractal it seems. When a range is not completed some of the largest gap pattern of the previous range is not filled in. I guess this could be measured by calculating the maximal gap size present, and observing it dropping on the completion of a range.
I left a web fiddle here which colors points according to which power of two range they are in, http://js.do/strainer/r2fill
I may use these ranges to create smooth non linear 2d surface fill pattern for modelling, which would be clipped to size. And same in 3d, maybe powers of three or 4 will be suitable.
Interesting post and very nice evaluation. Concerning the section on dithering: the blue noise comparison is not ideal. It seems you’re using a 64×64 blue noise mask, which is rather small; 256×256 masks are commonly used. A larger mask will have higher frequency response and result in less graininess in the dithered image. (The optimization process generating the mask obviously makes a difference, too.) Then, the regular structure of your R2 sequence will be more distracting to the human visual system than the graininess of blue noise.
Having said that, precomputed masks are limited in resolution, by the bit-depth used for the mask and the size of the mask. Obviously both can be increased, but at the cost of storage and therefore cache efficiency. An 8-bit mask, e.g., cannot resolve between an input value of 0 and anything 254/255 are effectively 1. Thus, there is an open issue of locally uniform adaptive sampling of very low and very high densities (efficiently). I did some quick (visual, qualitative) experiments to (qualitatively) verify that, indeed, the R2 sequence better samples (in terms of sample spacing) these densities than a precomputed blue noise mask.
I would summarize that for color/greyscale visual dithering, a blue noise mask will produce the best results because regular structure to which the visual system is so sensitive is broken up, but that your sequences are very interesting for efficient adaptive sampling of density functions that have very low and very high densities.
Still it would be cool to have a single tool for both tasks. Have you considered alternative functions to eliminate the banding artifacts?
Thanks for the very detailed and helpful comments. You are right, I used the 64×64 as that is what those authors published, but maybe I should find a 256×256 blue noise mask and use that instead. Interesting comment about visual dithering vs adaptive sampling. Will definitely think further on this.
I have now updated the comparison by using a 256×256 blue noise masks. As you predicted, the blue noise mask is now much better.
Your comment is full of such valuable information. I have now substantially modified my section on dithering to reflect many of your comments. This includes using a 256-Blue noise masks. It also includes specific comments that the dither masks based on R2 is real-valued and therefore can be naturally adapted to arbitrary bit depth. As you say, this latter point might offer substantial advantages for applications such as adaptive sampling.
Glad to hear it, and I like the changes you’ve added.
It seems part of my original post got clipped, but you understood anyways. In case it seems a bit confusing to someone else, the sentence concerning bit depth should read: “An 8-bit mask, e.g., cannot resolve between an input value of 0 and any other input value below 1/255…”
Concerning breaking up the regularity in the dither, one thing I thought of, but haven’t tried, is to add a small random offset to (x,y) that is constant for each small (e.g. 5×5) block in the image. It is a bit of a hack, and requires an additional random number, but should maintain the good properties while breaking up the regularity. Again, note that regularity is only an issue in certain applications.
If I understand your examples correctly, a regular grid would beat all the quasi-random sequences. From such a sequence you want uniformly distributed points, but also a lack of patterns. I am not aware of any particular test for these, I guess your Lena example is going in that direction, but I think you need something more thorough.
Good stuff! One comment on notation: I think you mean ‘cos(lambda – pi/2) = 2 u – 1’ (or just ‘sin(lambda) = 2 u – 1’ ), instead of ‘cos(lambda) = (2u – 1) – pi/2’ in the ‘Points on a sphere’ section.
Good pick up. Now fixed. Thanks.
Is there a paper that we can cite if using this method in our work?
Hi Aaron,
Glad to hear that this might be useful for you!
No, there is no published paper. As I do not work in academia, or for a company that supports publications, I suspect that I don’t have the credentials to publish in a journal. 🙁
So from my perspective, citing this blog post would be sufficient.
May I ask what work are you considering incorporating this into?
Hi Martin, thanks for getting back so quickly. We have found a useful application for this in building large-scale functional models of the brain (using the software Nengo and a mathematical framework called the NEF which has its roots in physics and control theory). In order to train these networks efficiently (e.g., up to 6.6 million neurons, recurrently connected) we rely on efficient procedures for sampling high-dimensional spaces for all of the regularized least-square optimization problems, and to uniformly tile the weights that encode low-dimensional state-spaces into these high-dimensional spaces. I’m using the methods of K-T. Fang (1994) to project your sequence (as well as Sobol’s) from the n-cube onto the n-ball and (n+1)-sphere. The code used to do this can be found here (https://github.com/arvoelke/nengolib/pull/153) and is exposed by Python calls to `nengolib.stats.ball` and nengolib.stats.sphere`. I will be citing this blog post. 🙂
by the way, i loved your short article on sampling from the n-ball and (n+1)-sphere. It was very ingenious.
Thanks! I’m surprised you found that. We’ve ended up using that method as a way to know, ahead of time, the one-dimensional projection of a distribution of vectors from the (n+1)-sphere. The memory model of Gosmann (2018) in particular uses this as a way to optimize what each neuron encodes, since it receives a one-dimensional projection of a random vector on average. Just in case you are curious as to how all of this fits in.
You pointed out that (in two dimensions) for the appropriate generalized Fibonacci numbers of points, the Delaunay triangulation – and, hence, the Voronoi diagram – gives what amounts to a quasiperiodic tiling by a constant number of tile types Presumably this also holds in higher dimensions. Have you looked into what the resulting tile shapes are? I wonder how this might relate to e.g. the Kelvin problem of finding regular honeycombs with low boundary measure.
Hi Robin,
Only a little bit. I have always expected (hoped?) it would hold for higher dimensions but to be honest I was struggling to work out advanced details for even the 2-dimensional case so I felt I had little hope of pinning down the equivalent constant shapes in 3-D. (For example, I can numerical calculate the empirical lengths of the sides of the tiling triangles, but I have so far not been able to express them in exact algebraic form….)
You have inspired me to have another crack at it — maybe I will find a technique related to the Kelvin problem that will magically help me in this exploration.
ps My PhD supervisor received his PhD from Imperial College many many years ago…. seems to be an amazing place to study!
😉
Very interesting read, thanks for sharing!
Very nice read, thanks Martin!
The R2 pattern looked so good, I had to try it out immediately. Unfortunately, while the point distribution is excellent in 2D, the 1D projections of the points (i.e. the individual 1D sequences for the x and y coordinates) have quite poor stratification. Here is a screenshot of the first 16 points in the sequence: https://imgur.com/QFm7rmc . Both x and y are quite far from uniform . This means that if the function you’re integrating has more variation along one axis, the error with this sequence will be worse than Halton or Sobol. I wonder if the star discrepancy captures this. Have you measured discrepancy?
Hi Iliyan,
Thanks for your comments and exploration.
Yes, it is a common challenge among quasirandom numbers that their projections on to lower dimensional spaces are not well distributed. And my R2 sequence is no different.
Similarly, most 2D quasirrandom sequences that have excellent 1D projections generally have a sub-optimal 2D distribution.
It seems like most things in life, you have to decide what you wish to optimize for! 😉
(Intuitively, the better the 2D distribution is, the closer it will be to the optimal 2D distribution which is the hexagonal packing, which has clear structure/stratification, and hence worse 1D projections.)
I am continuing exploration, along with many of my fellow gfx friends, to find sequences that have a balance of near-optimal 1D and 2D distributions, so watch this space
(or even better,… if you discover anything useful, I would love to hear about it!)
Martin
Great work 🙂
Thanks
Very interesting post!
Was a bit confused about what you said above figure 12 with “One can see that, as a consequence of ‘the curse of dimensionality’, the random distribution is better than all the low discrepancy sequences — except the R5-sequence.”
The following plot (figure 12) shows random (purple) mostly below all of the other sequences, which I take to mean that it has the worst packing distance, not the second best. Am I misinterpreting something?
I am also interested in how you computed your min(d_i) metric. My gut feeling tells me it has to be a brute force comparison between all of the points, which should be very slow.
Alexei
Hi Alexei,
Thanks for your interest and comments.
by the way, I used Mathematica to calculate min(d_i) which internally uses a highly optimized nearest-neigbor algorithm.
Martin