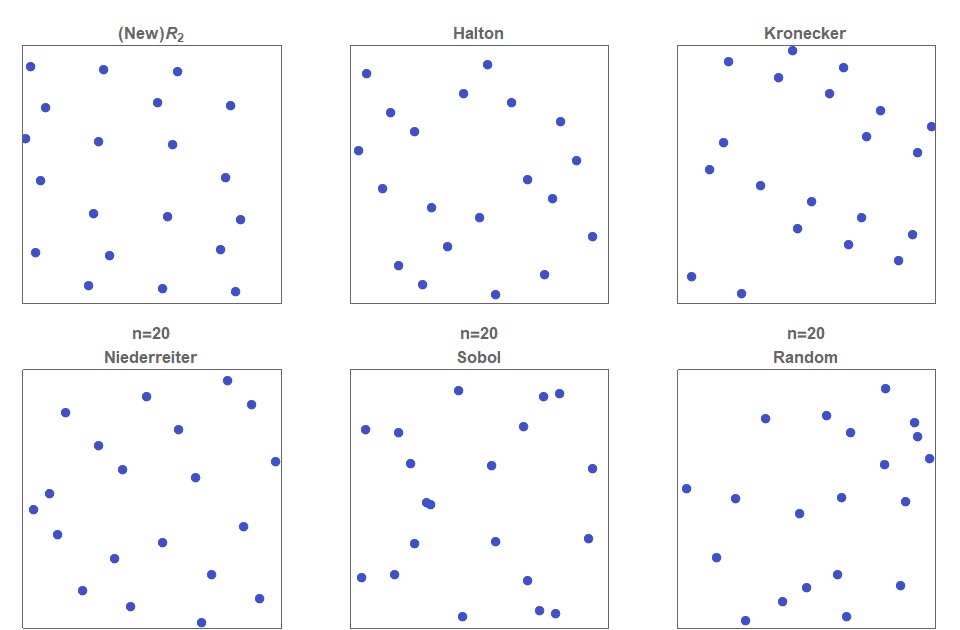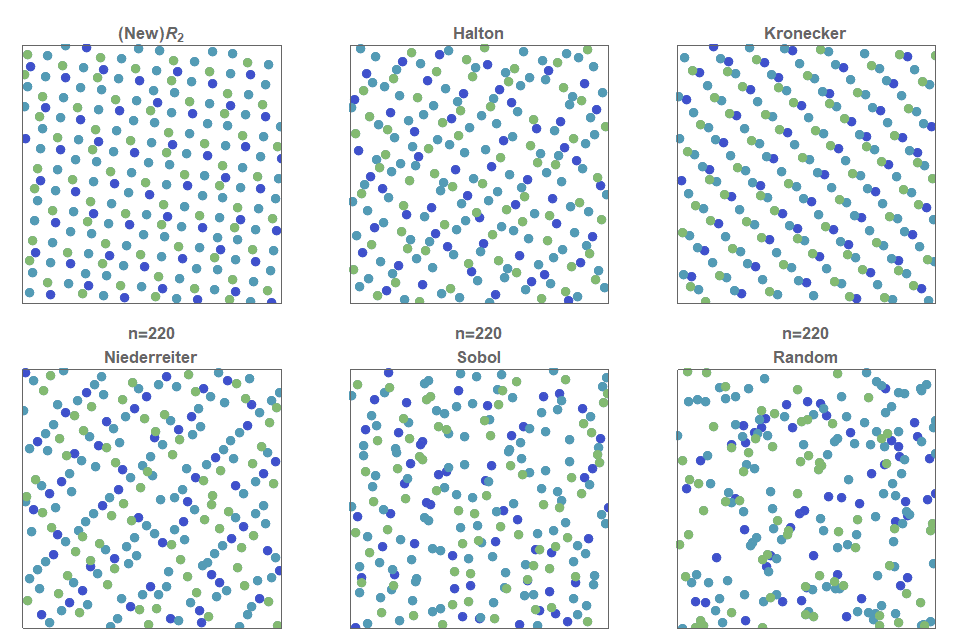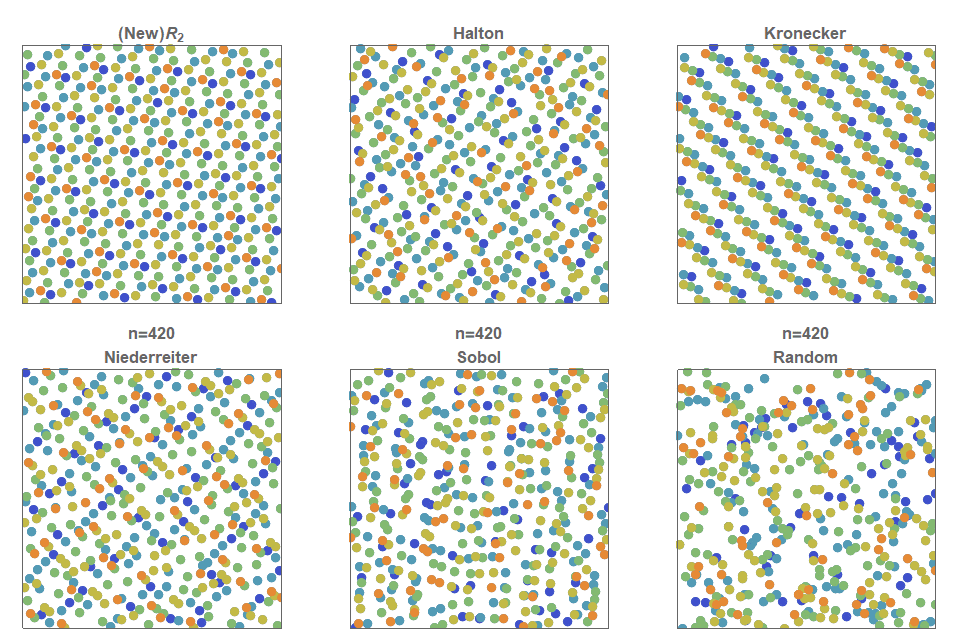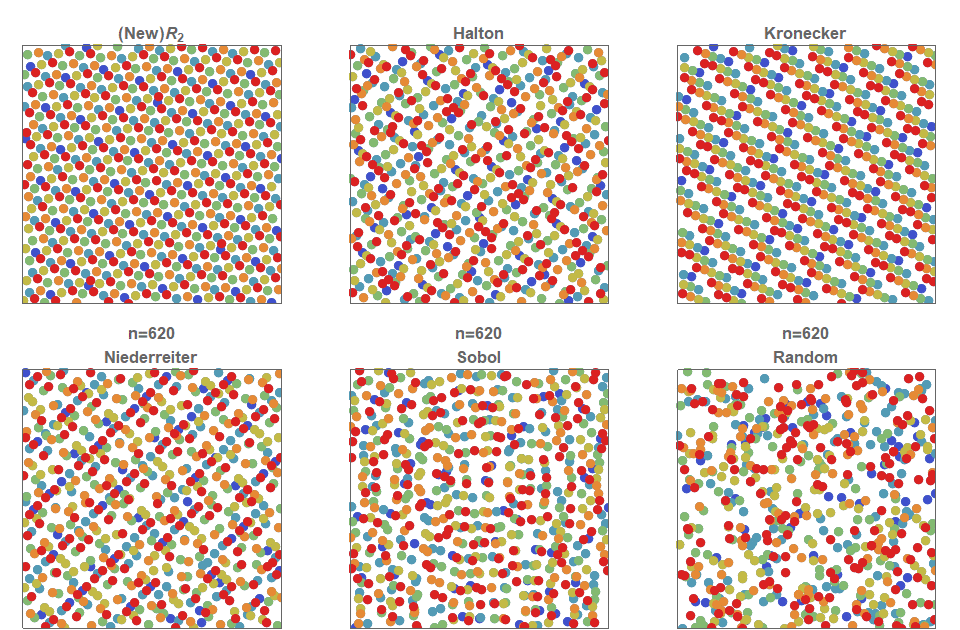
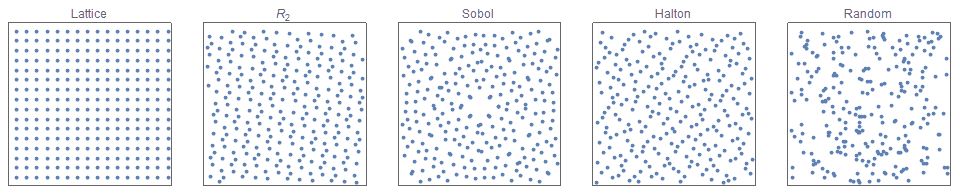
I present a new low discrepancy quasirandom sequence that offers many substantial improvements over other popular sequences such as the Sobol and Halton sequences.
Continue reading “The Unreasonable Effectiveness of Quasirandom Sequences”
Always curious. Always learning.
I present a new low discrepancy quasirandom sequence that offers many substantial improvements over other popular sequences such as the Sobol and Halton sequences.

Continue reading “The Unreasonable Effectiveness of Quasirandom Sequences”
When points are placed in a canonical grid layout, they are well-separated and their projections are uniform. I present a simple canonical grid layout which offers better closest-neighbor characterisics than the two most common contemporary canonical layouts.

Continue reading “An alternate canonical grid layout with uniform projections”
I describe a how a small but critical modification to correlated multi-jittered sampling can significantly improve its blue noise spectral characteristics whilst maintaining its uniform projections. This is an exact and direct grid-based construction method that guarantees a minimum neighbor point separation of at least $0.707/n$ and has an average point separation of $0.965/n$.

I describe a simple method for constructing a sequence of points, that is based on a low discrepancy quasirandom sequence but exhibits enhanced isotropic blue noise properties. This results in fast convergence rates with minimal aliasing artifacts.
Continue reading “A simple method to construct isotropic quasirandom blue noise point sequences”
Most two dimensional quasirandom methods focus on sampling over a unit square. However, sampling evenly over the triangle is also very important in computer graphics. Therefore, I describe a simple and direct construction method for a point sequence to evenly cover an arbitrary shaped triangle.

Continue reading “Evenly Distributing Points in a Triangle.”
I describe a probabilistic alternative to fractional factorial design based on the Sobol’ low discrepancy quasirandom sequence. This method is robust to aliasing (confounders), is often simpler to implement than traditional fractional factorial sample designs, and produces more accurate results than simple random sampling.
Continue reading “A probabilistic approach
to fractional factorial design”
In this brief post, I describes various methods to estimate uncertainty levels associated with numerical approximations of integrals based on quasirandom Monte Carlo (QMC) methods.