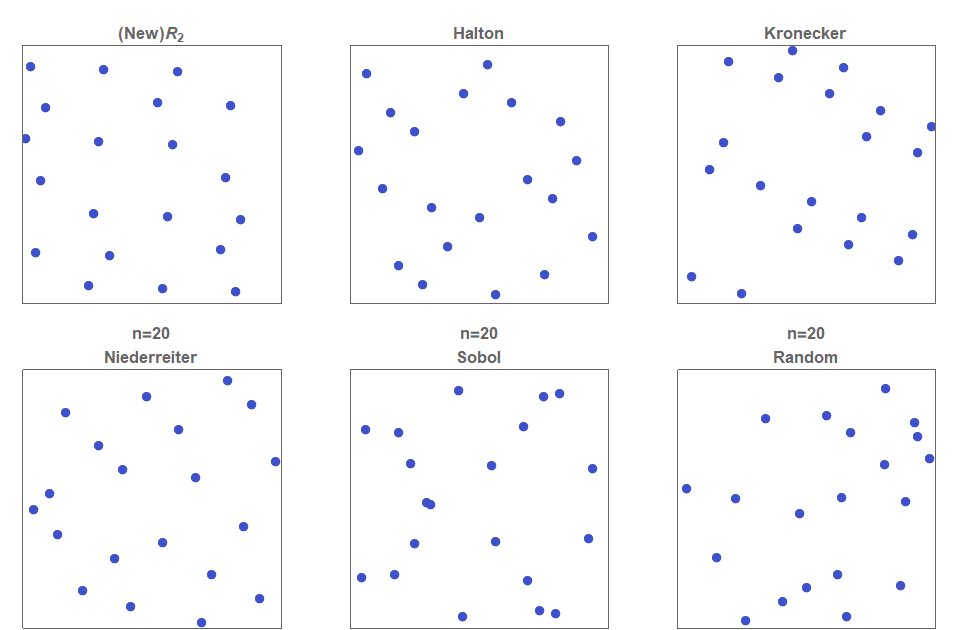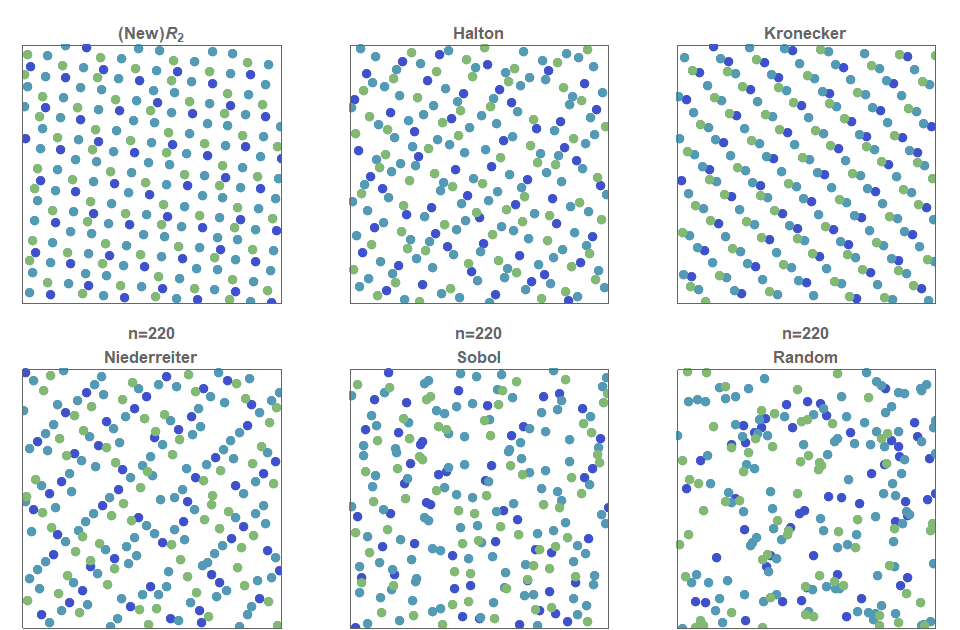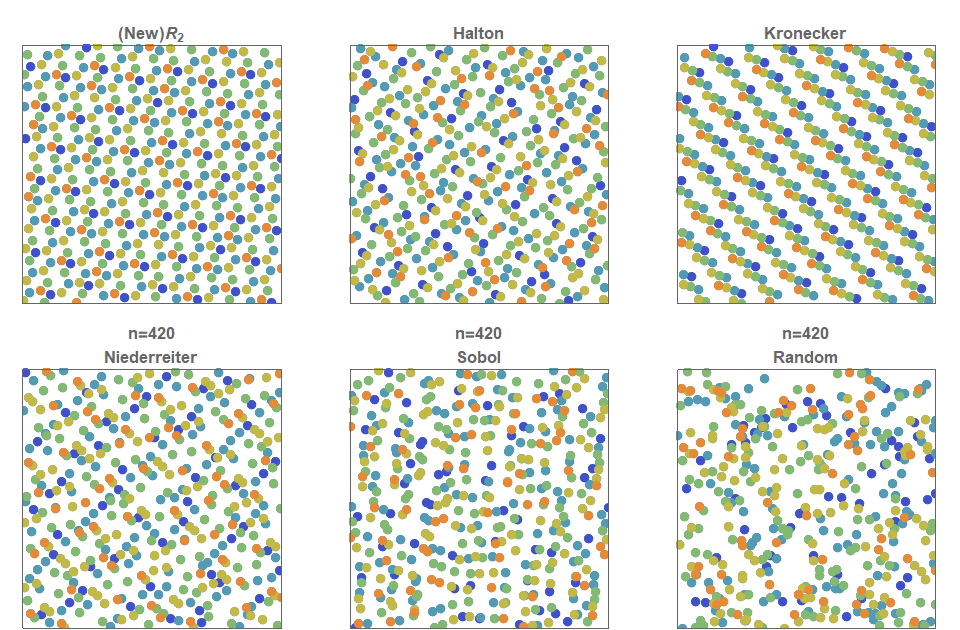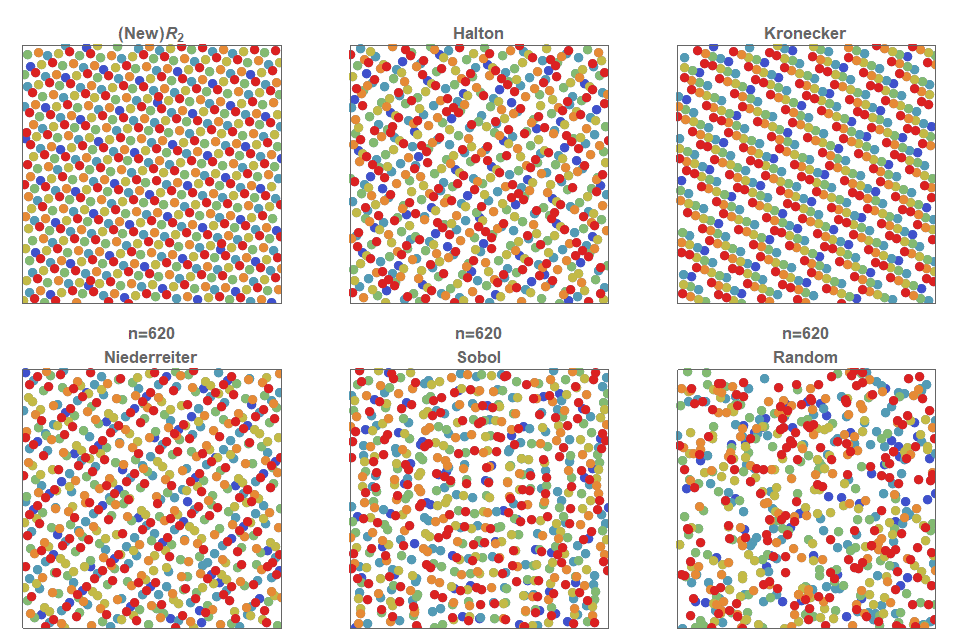
I present a new low discrepancy quasirandom sequence that offers many substantial improvements over other popular sequences such as the Sobol and Halton sequences.
Continue reading “The Unreasonable Effectiveness of Quasirandom Sequences”
Always curious. Always learning.
I present a new low discrepancy quasirandom sequence that offers many substantial improvements over other popular sequences such as the Sobol and Halton sequences.

Continue reading “The Unreasonable Effectiveness of Quasirandom Sequences”
I propose a new algorithm for multi-armed bandits, that is fully deterministic, as fast and simple to implement as UCB1, and yet, for a very broad range of practical circumstances empirically outperforms many of the existing industry standard Bernoulli multi-armed bandit policies, including Thompson Sampling and UCB-tuned.

Mapping the Fibonacci lattice (aka Golden Spiral, aka Fibonacci Sphere) onto the surface of a sphere is an extremely fast and effective approximate method to evenly distribute points on a sphere. I show how small modifications to the canonical implementation can result in notable improvements for nearest-neighbor measures.

For many Monte Carlo methods, such as those in graphical computing, it is critical to uniformly sample from $d$-dimensional spheres and balls. This post describes over twenty different methods to uniformly random sample from the (surface of) a $d$-dimensional sphere or the (interior of) a $d$-dimensional ball.
Continue reading “How to generate uniformly random points
on n-spheres and in n-balls”
I show that for the same reason that the golden ratio, $\phi=1.6180334..$, can be considered the most irrational number, that $1+\sqrt{2}$ can be considered the 2nd most irrational number, and indeed why $(9+\sqrt{221})/10$ can be considered the 3rd most irrational number.

Bridson’s Algorithm (2007) is a very popular method to produce maximal ‘blue noise’ sample point distributions such that no two points are closer than a specified distance apart. In this brief post we show how a minor modification to this algorithm can make it up to 20x faster and allows it to produce much higher density blue noise sample point distributions.

Continue reading “Maximal Poisson disk sampling:
an improved version of Bridson’s algorithm”
I describe a how a small but critical modification to correlated multi-jittered sampling can significantly improve its blue noise spectral characteristics whilst maintaining its uniform projections. This is an exact and direct grid-based construction method that guarantees a minimum neighbor point separation of at least $0.707/n$ and has an average point separation of $0.965/n$.

I describe a simple method for constructing a sequence of points, that is based on a low discrepancy quasirandom sequence but exhibits enhanced isotropic blue noise properties. This results in fast convergence rates with minimal aliasing artifacts.

Continue reading “A simple method to construct isotropic quasirandom blue noise point sequences”
Most two dimensional quasirandom methods focus on sampling over a unit square. However, sampling evenly over the triangle is also very important in computer graphics. Therefore, I describe a simple and direct construction method for a point sequence to evenly cover an arbitrary shaped triangle.

Continue reading “Evenly Distributing Points in a Triangle.”
When points are placed in a canonical grid layout, they are well-separated and their projections are uniform. I present a simple canonical grid layout which offers better closest-neighbor characterisics than the two most common contemporary canonical layouts.

Continue reading “An alternate canonical grid layout with uniform projections”
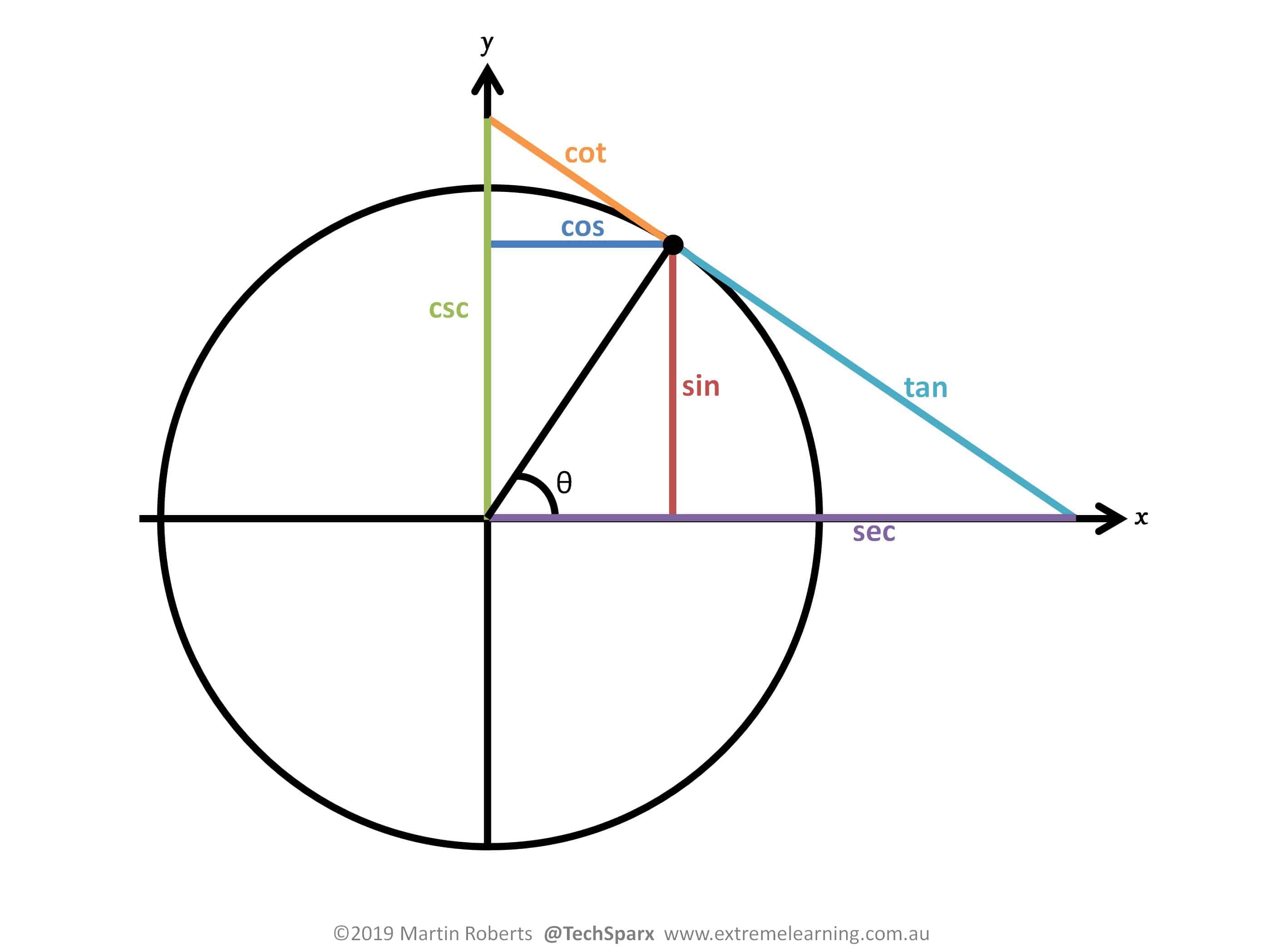
This post shows how the core trigonometric definitions, relations and addition theorems can be simply and intuitively visualized.
Unlike for circles, there isn’t a simple exact closed formula for the perimeter of an ellipse. We compare several well-known approximations, and conclude that a formula discovered by Ramanujan is our favourite, due to its simplicity and extreme accuracy.
![]()
Continue reading “A Formula for the Perimeter of an Ellipse”
This post illustrates and explains the beautiful Lissajous Curves – trajectories of points whose coordinates follow sinusoidal movements. A simple but timeless classic curve that has numerous applications as well as artistic elegance.
![]()
If you are given the initial terms of a sequence, then here is an insanely simple method to derive a general formula for the first N terms, as well as the sum of the first N terms of the sequence.
![]()
Continue reading “A simple formula for Sequences and Series”
I describe a probabilistic alternative to fractional factorial design based on the Sobol’ low discrepancy quasirandom sequence. This method is robust to aliasing (confounders), is often simpler to implement than traditional fractional factorial sample designs, and produces more accurate results than simple random sampling.
![]()
Continue reading “A probabilistic approach
to fractional factorial design”
The Theil-Sen (Kendall) and Siegel estimators are non-parametric distribution-free methods used to fit a line to data, in ways that are very robust to large levels of noise and outliers. We briefly illustrate how the lesser-known Siegel estimator is typically better than the more commonly used Theil-Sen estimator.
Continue reading “The Theil-Sen and Siegel non-parametric estimators
for linear regression”
This fun post illustrates the phenomenon of multiple uncoupled pendulums whose periods are all rational multiples of each other.

In this brief post, I describes various methods to estimate uncertainty levels associated with numerical approximations of integrals based on quasirandom Monte Carlo (QMC) methods.
Creating unbiased random permutations of lists is often crucial to sampling. The Fisher-Yates shuffle is the definitive method to shuffle a sequence of items. Popularised by Knuth, it is unbiased, has optimal linear time efficiency; uses constant space; and is incremental.
How to distribute points on the surface of a sphere as evenly as possibly is an incredibly important problem in maths, science and computing, and mapping the Fibonacci lattice onto the surface of a sphere via equal-area projection is an extremely fast and effective approximate method to achieve this. I show that with only minor modifications it can be made even better.
![]()